题目内容
已知a=(log54)2,b=log53,c=ln
,下列结论正确的是( )
| 3 |
| A、a>c>b |
| B、a>b>c |
| C、c>a>b |
| D、b>a>c |
考点:对数值大小的比较
专题:函数的性质及应用
分析:利用基本不等式的性质可得(log54)2=
>log53•log5
;利用对数换底公式可得c=ln
=
<log53,即可得出.
(log53+log5
| ||
| 4 |
| 16 |
| 3 |
| 3 |
log5
| ||
| log5e |
解答:
解:∵a=(log54)2=
>log53•log5
>log53=b,∴a>b;
∵e2>5,∴log5e2>log55=1,
∴c=ln
=
=
<log53=b,
∴a>b>c.
故选:B.
(log53+log5
| ||
| 4 |
| 16 |
| 3 |
∵e2>5,∴log5e2>log55=1,
∴c=ln
| 3 |
log5
| ||
| log5e |
| log53 |
| log5e2 |
∴a>b>c.
故选:B.
点评:本题考查了基本不等式的性质、对数的运算法则及其换底公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
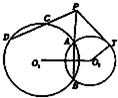 如图,⊙O1与⊙O2相交于A,B两点,点P在线段BA延长线上,T是⊙O1上一点,PT⊥O2T,过P的直线交⊙O1于C,D两点
如图,⊙O1与⊙O2相交于A,B两点,点P在线段BA延长线上,T是⊙O1上一点,PT⊥O2T,过P的直线交⊙O1于C,D两点