题目内容
12.求下列函数的导数:(1)y=$\frac{1}{\sqrt{x}}$•cosx;
(2)y=x(x2+$\frac{1}{x}+\frac{1}{{x}^{3}}$)
分析 利用求导法则即可求其导数.
解答 解:(1)$y′=\frac{-\sqrt{x}sinx-\frac{1}{2}{x}^{-\frac{1}{2}}cosx}{(\sqrt{x})^{2}}$=$\frac{-2xsinx-cosx}{2(\sqrt{x})^{3}}$
∴y′=$\frac{-2xsinx-cosx}{2(\sqrt{x})^{3}}$
(2)∵$y={x}^{3}+1+\frac{1}{{x}^{2}}$,
∴$y′={x}^{2}-\frac{2}{{x}^{3}}$
点评 本题考查导数的求导法则,属于基础题.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
7.已知函数f(x)=$\frac{1}{3}$x3-(1+$\frac{b}{2}$)x2+2bx在区间(-3,1)上是减函数,则实数b的取值范围是( )
| A. | (-∞,-3] | B. | (-∞,1] | C. | [1,2] | D. | [-3,+∞) |
5.已知某大城市对每人车流量拥挤等级规定如表:
该城市对国庆节7天的车流量作出如表的统计数据:
(1)求该城市国庆节期间车流量的平均值与方差;
(2)某人国庆节连续2天到该城市游玩,求这2天他遇到的车流量拥挤等级均为严重拥挤的概率.
| 车流量(万辆) | 0~10 | 11~50 | 51~70 | 71~80 | 81~100 | >100 |
| 拥挤等级 | 优 | 良 | 轻度拥挤 | 中度拥挤 | 重度拥挤 | 严重拥挤 |
| 日期 | 10月1日 | 10月2日 | 10月3日 | 10月4日 | 10月5日 | 10月6日 | 107日 |
| 车流量(万辆) | 120 | 110 | 85 | 75 | 60 | 105 | 110 |
(2)某人国庆节连续2天到该城市游玩,求这2天他遇到的车流量拥挤等级均为严重拥挤的概率.
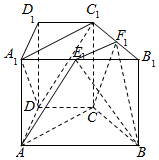 如图,在棱柱ABCD-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD为直角梯形,其中AB∥CD,AB⊥AD,AB=AC=2CD=2,AA1=$\sqrt{3}$,过AC的平面分别与A1B1,B1C1交于E1,F1,且E1为A1B1的中点.
如图,在棱柱ABCD-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD为直角梯形,其中AB∥CD,AB⊥AD,AB=AC=2CD=2,AA1=$\sqrt{3}$,过AC的平面分别与A1B1,B1C1交于E1,F1,且E1为A1B1的中点.