已知等比数列{an}的公比为-$\frac{1}{2}$.则$\frac{{a} {1}+{a} {3}+{a} {5}}{{a} {2}+{a} {4}+{a} {6}}$的值是-2．题目和参考答案——青夏教育精英家教网—

题目内容

7．已知等比数列{a_n}的公比为-$\frac{1}{2}$，则$\frac{{a}_{1}+{a}_{3}+{a}_{5}}{{a}_{2}+{a}_{4}+{a}_{6}}$的值是-2．

分析由题意整体可得$\frac{{a}_{1}+{a}_{3}+{a}_{5}}{{a}_{2}+{a}_{4}+{a}_{6}}$=$\frac{{a}_{1}+{a}_{3}+{a}_{5}}{{a}_{1}q+{a}_{3}q+{a}_{5}q}$=$\frac{1}{q}$，代值计算可得．

解答解：∵等比数列{a_n}的公比q=-$\frac{1}{2}$，
∴$\frac{{a}_{1}+{a}_{3}+{a}_{5}}{{a}_{2}+{a}_{4}+{a}_{6}}$=$\frac{{a}_{1}+{a}_{3}+{a}_{5}}{{a}_{1}q+{a}_{3}q+{a}_{5}q}$=$\frac{1}{q}$=-2
故答案为：-2

点评本题考查等比数列的通项公式，涉及整体思想，属基础题．

练习册系列答案

小学毕业升学复习必做的18套试卷系列答案

18．

如图，在同一平面内，∠AOB=150°，∠AOC=120°，|$\overrightarrow{OA}$|=2，|$\overrightarrow{OB}$|=3，|$\overrightarrow{OC}$|=4．
（1）试用$\overrightarrow{OB}$和$\overrightarrow{OC}$表示$\overrightarrow{OA}$；
（2）是否存在实数λ，使得$\overrightarrow{AD}$=$λ\overrightarrow{AC}$，$\overrightarrow{AC}$$•\overrightarrow{BD}$=0同时成立？若存在，求出λ的值，若不存在，请说明理由．

15．在二项式（x+2）ⁿ的展开式中只有第4项的系数最大，求第3项．

2．若log_ab=c，则a，b，c之间满足（　　）

12．求下列函数的导数：
（1）y=$\frac{1}{\sqrt{x}}$•cosx；
（2）y=x（x²+$\frac{1}{x}+\frac{1}{{x}^{3}}$）

2．

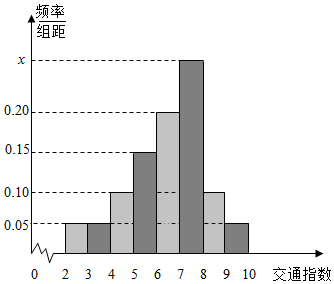交通指数是指交通拥堵指数或交通运行指数（Traffic Performance Index，即“TPI”），是反应道路畅通或拥堵的概念性数值，交通指数的取值范围为0～10，分为五级：0～2畅通，2～4为基本畅通，4～6轻度畅通，6～8为中度拥堵，8～10为严重拥堵．高峰时段，巴中市交通指挥中心随机选取了市区40个交通路段，依据交通指数数据绘制的频率分布直方图如图所示：
（Ⅰ）求出图中x的值，并计算这40个路段中为“中度拥堵”的有多少个？
（Ⅱ）在我市区的40个交通路段中用分层抽样的方法抽取容量为20的样本．从这个样本路段的“基本畅通”和“严重拥堵”路段中随机选出2个路段，求其中只有一个是“严重拥堵”路段的概率．

19．下列说法中：
①任取x₁，x₂∈I（区间），当x₁＜x₂时，f （x₁）＜f （x₂），则y=f （x）在I上是增函数；
②函数y=x²在R上是增函数；
③函数y=$\left\{\begin{array}{l}{x+3，x≥0}\\{-{x}^{2}，x＜0}\end{array}\right.$在定义域上是增函数；
④y=$\frac{1}{x}$的单调递减区间是（-∞，0）∪（0，+∞）．
正确的序号为①③．

20．若关于x的不等式4^x+x-a≤$\frac{3}{2}$在x∈（0，$\frac{1}{2}$]上恒成立，则实数a的取值范围是（　　）

试题分类