题目内容
7．已知函数f（x）=$\frac{1}{3}$x3-（1+$\frac{b}{2}$）x2+2bx在区间（-3，1）上是减函数，则实数b的取值范围是（ ）| A． | （-∞，-3] | B． | （-∞，1] | C． | [1，2] | D． | [-3，+∞） |
分析 若函数f（x）=$\frac{1}{3}$x3-（1+$\frac{b}{2}$）x2+2bx在区间（-3，1）上是减函数，则f′（x）=x2-（2+b）x+2b=（x-b）（x-2）＜0在区间（-3，1）上恒成立，进而得到答案．
解答 解：∵函数f（x）=$\frac{1}{3}$x3-（1+$\frac{b}{2}$）x2+2bx在区间（-3，1）上是减函数，
∴f′（x）=x2-（2+b）x+2b=（x-b）（x-2）＜0在区间（-3，1）上恒成立，
即（-3，1）⊆（b，2），
解得：b≤-3，
实数b的取值范围是（-∞，-3]，
故选：A
点评 本题考查的知识点是利用导数解答函数的单调性问题，难度中档．
练习册系列答案
相关题目
14．下列命题中是全称命题且为真命题的序号为①③．
①圆有内接正方形，②$\sqrt{3}＞\sqrt{2}$，③指数函数都是单调函数，④常数列都是等比数列，⑤两个正数的算术平均数大于它们的几何平均数．
①圆有内接正方形，②$\sqrt{3}＞\sqrt{2}$，③指数函数都是单调函数，④常数列都是等比数列，⑤两个正数的算术平均数大于它们的几何平均数．
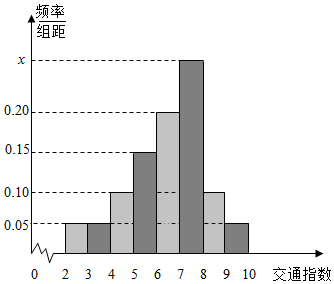交通指数是指交通拥堵指数或交通运行指数（Traffic Performance Index，即“TPI”），是反应道路畅通或拥堵的概念性数值，交通指数的取值范围为0～10，分为五级：0～2畅通，2～4为基本畅通，4～6轻度畅通，6～8为中度拥堵，8～10为严重拥堵．高峰时段，巴中市交通指挥中心随机选取了市区40个交通路段，依据交通指数数据绘制的频率分布直方图如图所示：
12．某校为调查2016届学业水平考试的数学成绩情况，随机抽取2个班各50名同学，得如下频率分布表：
（Ⅰ）估计甲，乙两班的数学平均分（同一组中的数据用该组区间的中点值作代表）；
（Ⅱ）数学成绩[60，70）为“C等”，[70，90）为“B等”和[90，100]为“A等”，从两个班成绩为“A等”的同学中用分层抽样的方法抽取5人，则甲乙两个班各抽取多少人？
（Ⅲ）从第（Ⅱ）问的5人中随机抽取2人，求这2人来自同一班级的概率．
| 分数段 | [50，60） | [60，70） | [70，80） | [80，90） | [90，100] |
| 甲班频数 | 4 | 6 | 10 | 18 | 12 |
| 乙班频数 | 2 | 6 | 18 | 16 | 8 |
（Ⅱ）数学成绩[60，70）为“C等”，[70，90）为“B等”和[90，100]为“A等”，从两个班成绩为“A等”的同学中用分层抽样的方法抽取5人，则甲乙两个班各抽取多少人？
（Ⅲ）从第（Ⅱ）问的5人中随机抽取2人，求这2人来自同一班级的概率．