题目内容
2.若满足$\left\{\begin{array}{l}{2x-y+1≥0}\\{x+2y-2≥0}\\{ax+by+c≤0}\end{array}\right.$,的点(x,y)所表示的区域能被直径为$\sqrt{10}$的圆完全覆盖,则区域D的面积最大值为$\frac{5}{2}$,当区域D的面积最大时,z=x-y最大值为2.分析 由题意作平面区域,易知BC⊥BA,从而可得当三角形内接于圆时,面积最大,从而求最大值及点A的坐标,从而求得.
解答 解:由题意作平面区域如下,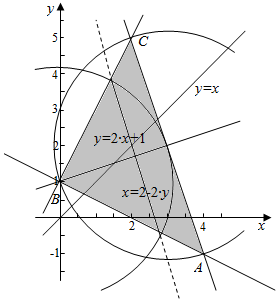
易知直线y=2x+1与直线x=2-2y互相垂直,即BC⊥BA;
故当三角形内接于圆时,面积最大,
故区域D的面积最大值为$\frac{1}{2}$×$\sqrt{10}$×$\frac{\sqrt{10}}{2}$=$\frac{5}{2}$,
故设A(2-2y,y),
|BA|=$\sqrt{(2-2y)^{2}+(y-1)^{2}}$=$\frac{\sqrt{10}}{\sqrt{2}}$,
解得,y=0或y=2(舍去);
故A(2,0),
故 z=x-y最大值为2-0=2,
故答案为:$\frac{5}{2}$,2.
点评 本题考查了线性规划的变形应用及数形结合的思想方法应用,属于中档题.

练习册系列答案
相关题目
12.集合A={x|x≤a},B={x|x2-5x<0},若A∩B=B,则a的取值范围是( )
| A. | a≥5 | B. | a≥4 | C. | a<5 | D. | a<4 |
13.已知数列{an}的首项a1=a,其前n项和为Sn,且满足Sn+Sn-1=3n2+2n+4(n≥2),若对任意的n∈N*,an<an+1恒成立,则a的取值范围是( )
| A. | ($\frac{23}{4}$,$\frac{29}{4}$) | B. | ($\frac{20}{3}$,$\frac{29}{4}$) | C. | ($\frac{23}{4}$,$\frac{20}{3}$) | D. | (-∞,$\frac{20}{3}$) |
7.函数f(x)=$\frac{π}{2}$-$\frac{sinx}{3+|x|}$的最大值是M,最小值是m,则f(M+m)的值等于( )
| A. | 0 | B. | 2π | C. | $\frac{π}{2}$ | D. | π |
14.下列命题中是全称命题且为真命题的序号为①③.
①圆有内接正方形,②$\sqrt{3}>\sqrt{2}$,③指数函数都是单调函数,④常数列都是等比数列,⑤两个正数的算术平均数大于它们的几何平均数.
①圆有内接正方形,②$\sqrt{3}>\sqrt{2}$,③指数函数都是单调函数,④常数列都是等比数列,⑤两个正数的算术平均数大于它们的几何平均数.
11.已知AB为圆C的弦,C为圆心,且|$\overrightarrow{AB}$|=2,则$\overrightarrow{AB}$$•\overrightarrow{AC}$=( )
| A. | -2 | B. | 2 | C. | $\sqrt{3}$ | D. | -$\sqrt{3}$ |