题目内容

已知函数f（x）=cos2（x-
π
6
）-sin2x，x∈[0，
π
2
]．
（1）求f（
π
12
）的值； 
（2）求f（x）的值域．
考点：三角函数中的恒等变换应用
专题：三角函数的求值
分析：（1）利用二倍角公式、辅助角公式化简函数，即可求f（
π
12
）的值；
（2）由x∈[0，
π
2
]知2x+
π
3
∈[
π
3
，
4π
3
]，可得-
3
2
≤sin（2x+
π
3
）≤1，从而可求f（x）的值域．
解答： 解：（1）函数f（x）=cos2（x-
π
6
）-sin2x=
1+cos(2x-
π
3
)
2
-
1-cos2x
2
…（2分）
=
1
2
[cos(2x-
π
3
)+cos2x]=
1
2
(
3
2
sin2x+
3
2
cos2x)…（4分）
=
3
2
(
1
2
sin2x+
3
2
cos2x)=
3
2
sin(2x+
π
3
)…（6分）
∴f（
π
12
）=
3
2
sin(
π
6
+
π
3
)=
3
2
sin
π
2
=
3
2
…（8分）
（2）由x∈[0，
π
2
]知2x+
π
3
∈[
π
3
，
4π
3
]…（9分）
∴-
3
2
≤sin（2x+
π
3
）≤1…（11分）
∴-
3
4
≤
3
2
sin(2x+
π
3
)≤
3
2
，
∴f（x）的值域为[-
3
4
，
3
2
]…（12分）
点评：本题考查三角函数的化简，考查三角函数的性质，正确化简函数，利用三角函数的性质是关键．
练习册系列答案
相关题目
曲线C1的参数方程为
x=cosθ
y=sinθ
（θ为参数），将曲线C1上所有点的横坐标伸长为原来的2倍，纵坐标伸长为原来的
3
倍，得到曲线C2．
（Ⅰ）求曲线C2的普通方程；
（Ⅱ）已知点B（1，1），曲线C2与x轴负半轴交于点A，P为曲线C2上任意一点，求|PA|2-|PB|2的最大值．
行列式
.
3
Acosx
A
2
-2Asinx0
11cosx
.
（A＞0）按第一列展开得
3
M11-2M21+M31，记函数f（x）=M11+M21，且f（x）的最大值是4．
（1）求A；
（2）将函数y=f（x）的图象向左平移
π
12
个单位，再将所得图象上各点的横坐标扩大为原来的2倍，纵坐标不变，得到函数y=g（x）的图象，求g（x）在(-
π
12
，
11π
12
)上的值域．
一个几何体的三视图如图所示，则这个几何体的体积是（　　）
A、1
B、2
C、
2
3
D、
1
3
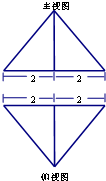三棱锥P-ABC的主视图和俯视图为如图所示的两个全等的等腰三角形，其中底边长为4，腰长为3，则该三棱锥左视图的面积为（　　）
A、
5
2
B、2
5
C、
5
D、5
已知点A（x1，f（x1）），B（x2，f（x2））是函数f（x）=2sin（ωx+φ）(ω＞0，-
π
2
＜φ＜0)图象上的任意两点，且角φ的终边经过点P(1，-
3
)，若|f（x1）-f（x2）|=4时，|x1-x2|的最小值为
π
3
．
（1）求函数f（x）的解析式；
（2）求函数f（x）的单调递增区间；
（3）当x∈[0，
π
6
]时，不等式mf（x）+2m≥f（x）恒成立，求实数m的取值范围．
（Ⅰ）若a是从1，2，3，4四个数中任取的一个数，b是从1，2，3三个数中任取的一个数，求点P（a，b）在椭圆
x2
16
+
y2
9
=1内的概率．
（Ⅱ）若a是从区间（0，3]任取的一个实数，b是从区间（0，3]任取的一个实数，求直线y=x+1与椭圆
x2
a2
+
y2
b2
=1有公共点的概率．
一几何体的三视图如下所示，则该几何体的表面积为
 
．
已知函数f（x）=
x-1
+
3-x

（1）计算f（
5
4
），f（
3
2
），f（
11
4
），f（
5
2
）的值，据此提出一个猜想，并予以证明；
（2）证明：除点（2，2）外，函数f（x）=
x-1
+
3-x
的图象均在直线y=2的下方．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网