题目内容
已知正四面体ABCD中，P为棱AD的中点，则过点P与面ABC和面BCD所在平面都成60°角的平面共有几个？（若二面角α-l-β的大小为120°，则平面α与β所成角也为60°）
考点：二面角的平面角及求法
专题：综合题,空间角
分析：在正四面体A-BCD中，取BC的中点E，连结AE，DE，则∠AED就是二面角A-BC-D的平面角，设过点P垂直于平面ABC的直线为m，过点P垂直于平面BCD的直线为n，则m与n所成角∈（
，
），可得过点P可作4条直线同时与直线m，n成
，即可得出结论．
| π |
| 3 |
| π |
| 2 |
| π |
| 3 |
解答：
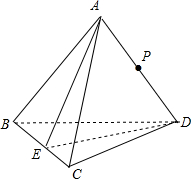解：在正四面体A-BCD中，取BC的中点E，连结AE，DE，
则∠AED就是二面角A-BC-D的平面角，在等腰三角形AED中，可求得cos∠AED=
，
∴二面角A-BC-D的余弦为
＜
，二面角A-BC-D∈（
，
），
设过点P垂直于平面ABC的直线为m，过点P垂直于平面BCD的直线为n，则m与n所成角∈（
，
），
∴过点P可作4条直线同时与直线m，n成
，
即符合题意的平面有4个．
解：在正四面体A-BCD中，取BC的中点E，连结AE，DE，则∠AED就是二面角A-BC-D的平面角，在等腰三角形AED中，可求得cos∠AED=
| 1 |
| 3 |
∴二面角A-BC-D的余弦为
| 1 |
| 3 |
| 1 |
| 2 |
| π |
| 3 |
| π |
| 2 |
设过点P垂直于平面ABC的直线为m，过点P垂直于平面BCD的直线为n，则m与n所成角∈（
| π |
| 3 |
| π |
| 2 |
∴过点P可作4条直线同时与直线m，n成
| π |
| 3 |
即符合题意的平面有4个．
点评：本题考查二面角的平面角及求法，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
相关题目
若A={2，4，6，8}，B={-1，-3，-5，-7}，下列对应关系
①f：x→9-2x，②f：x→1-x，③f：x→7-x，④f：x→x-9中，
能确定A到B的映射的是（ ）
①f：x→9-2x，②f：x→1-x，③f：x→7-x，④f：x→x-9中，
能确定A到B的映射的是（ ）
| A、①② | B、②③ | C、③④ | D、②④ |
若x∈A，且
∈A，则称A是“伙伴关系集合”．在集合M={-1，0，
，
，
，1，2，3，4}的所有非空子集中任选一个集合，则该集合是“伙伴关系集合”的概率为（ ）
| 1 |
| x |
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
中心城区现有绿化面积为1000hm2，计划每年增长4%，经过x（x∈N*）年，绿化面积为y hm2，则x，y间的函数关系式为（ ）
| A、y=1000（1+4%）x（x∈N*） |
| B、y=（1000×4%）x（x∈N*） |
| C、y=1000（1-4%）x （x∈N*） |
| D、y=1000（4%）x（x∈N*） |
图①是一个边长为（m+n）的正方形，小明将图①中的阴影部分拼成图②的形状，由图①和图②能验证的式子是（ ）| A、（m+n）2-（m-n）2=4mn |
| B、（m+n）2-（m2+n2）=2mn |
| C、（m-n）2+2mn=m2+n2 |
| D、（m+n）（m-n）=m2-n2 |
设集合S={y|y=（
）x-1，x∈R}，T={y|y=log2（x+2）}，S∪T=（ ）
| 1 |
| 2 |
| A、S | B、T |
| C、R | D、[-1，+∞） |