题目内容
求函数的单调递增区间:y=lgsin(
-2x).
| π |
| 6 |
考点:复合函数的单调性
专题:计算题,函数的性质及应用,三角函数的图像与性质
分析:先根据复合函数的单调性把问题转化为求t=sin(
-2x)=-sin(2x-
)的大于0的增区间,即求y=sin(2x-
)的小于0的减区间.
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
解答:
解:由复合函数的单调性知,
求y=lgsin(
-2x)的单调增区间,即求t=sin(
-2x)=-sin(2x-
)的大于0的增区间,即求y=sin(2x-
)的小于0的减区间,
∴2kπ-π<2x-
≤2kπ-
,解得kπ-
<x≤kπ-
,k∈z,
∴函数y=lgsin(
-2x)的单调增区间为(kπ-
,kπ-
],k∈z.
求y=lgsin(
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
∴2kπ-π<2x-
| π |
| 6 |
| π |
| 2 |
| 5π |
| 12 |
| π |
| 6 |
∴函数y=lgsin(
| π |
| 6 |
| 5π |
| 12 |
| π |
| 6 |
点评:该题主要考查复合函数的单调性、三角函数的单调性,正确理解“同增异减”的含义是解题关键,解答该题容易忽略求定义域导致出错.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列函数与y=x有相同图象的一个函数是( )
A、y=
| ||
B、y=
| ||
| C、y=logaax | ||
| D、y=a logax(a>0且a≠1) |
已知集合A={x|x<a},B={x|2<x<4},且A∪(∁RB)=R,则实数a的取值范围( )
| A、a≤4 | B、a<2 |
| C、a>4 | D、a≥4 |
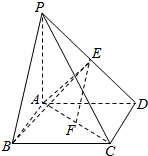 如图所示,在四棱锥P-ABCD中,底面ABCD为正方形,侧棱PA⊥底面ABCD,PA=AD=1,E,F分别为PA、AC的中点.
如图所示,在四棱锥P-ABCD中,底面ABCD为正方形,侧棱PA⊥底面ABCD,PA=AD=1,E,F分别为PA、AC的中点.