题目内容
在△ABC中,DEF为BC、AC、AB上的点,
=
,
=
,
=λ(
+
),
•
=
•
,
=μ(
+
),则
= .
| AF |
| 2 |
| 3 |
| AB |
| AE |
| 3 |
| 4 |
| AC |
| AD |
| ||
|
|
| ||
|
|
| DE |
| AD |
| DE |
| CD |
| DF |
| ||
|
|
| ||
|
|
|
| ||
|
|
考点:向量加减混合运算及其几何意义
专题:综合题,平面向量及应用
分析:由题意得出
⊥
,
⊥
,
⊥
,得A,E,D,F四点共圆,证明△AEF∽△ABC,求出
=
=
的值,即得结果.
| BC |
| AD |
| DE |
| AC |
| BA |
| DF |
| EF |
| BC |
| AE |
| AB |
| AF |
| AC |
解答:
解:如图所示,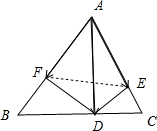
∵
=λ(
+
),
∴
•
=λ[
+
]=0,
∴
⊥
,即BC⊥AD;
∵
•
=
•
,
∴
•(
-
)=0,
∴
•(
-
)=0,
即
•
=0,
∴
⊥
,即DE⊥CA;
又∵
=μ(
+
),
∴
•
=μ[
+
]=0,
∴
⊥
,即BA⊥DF;
连接EF,∵DE⊥AC,DF⊥AB,
∴A,E,D,F四点共圆,∴∠AEF=∠ADF;
又∵AD⊥BC,∴∠B=∠ADF,
∴∠B=∠AEF,
∴△AEF∽△ABC;
∴
=
=
,
∵
=
,
=
,
∴
=
,即AC=
AB;
∴
=
=
=
=
,
∴
=
.
故答案为:
.

∵
. |
| AD |
| ||
|
|
| ||
|
|
∴
| BC |
| AD |
|
| ||||
|
|
|
| ||||
|
|
∴
| BC |
| AD |
∵
| DE |
| AD |
| DE |
| CD |
∴
| DE |
| AD |
| CD |
∴
| DE |
| DC |
| DA |
即
| DE |
| AC |
∴
| DE |
| AC |
又∵
| DF |
| ||
|
|
| ||
|
|
∴
| BA |
| DF |
|
| ||||
|
|
|
| ||||
|
|
∴
| BA |
| DF |
连接EF,∵DE⊥AC,DF⊥AB,
∴A,E,D,F四点共圆,∴∠AEF=∠ADF;
又∵AD⊥BC,∴∠B=∠ADF,
∴∠B=∠AEF,
∴△AEF∽△ABC;
∴
| EF |
| BC |
| AE |
| AB |
| AF |
| AC |
∵
| AF |
| 2 |
| 3 |
| AB |
| AE |
| 3 |
| 4 |
| AC |
∴
| ||
| AB |
| ||
| AC |
2
| ||
| 3 |
∴
| EF |
| BC |
| AE |
| AB |
| ||
| AB |
| ||||||
| AB |
| ||
| 2 |
∴
|
| ||
|
|
| 2 |
故答案为:
| 2 |
点评:本题考查了向量垂直与数量积的关系、四点共圆的判定定理、相似三角形的判定与性质、向量共线定理等基础知识与基本技能方法,考查了分析问题和解决问题的能力,考查了推理能力和计算能力,是难题.

练习册系列答案
相关题目
下列函数中,与函数y=x相同的函数是( )
A、y=
| ||||
B、y=(
| ||||
| C、y=lg10x | ||||
| D、y=2log2x |
已知向量
=(1,-2),
=(-
,y),若
∥
,则y=( )
| a |
| b |
| 1 |
| 2 |
| a |
| b |
| A、1 | B、-1 | C、2 | D、-2 |
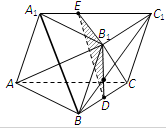 如图,在三棱柱ABC-A1B1C1中,D是BC的中点.
如图,在三棱柱ABC-A1B1C1中,D是BC的中点.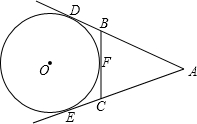 如图:AE、AD、BC分别切⊙O于E、D、F,若AD=14,则△ABC的周长为
如图:AE、AD、BC分别切⊙O于E、D、F,若AD=14,则△ABC的周长为