题目内容
若函数y=acosx+b(a,b为常数)的最大值为1,最小值为-7,求函数y=3+absinx的最值和最小正周期.
考点:余弦函数的图象
专题:三角函数的图像与性质
分析:首先,要分a>0和a<0两种情形进行讨论,然后,分别求解最值和最小正周期即可.
解答:
解:当a>0时,cosx=-1时取得最小值-a+b=-7,
cosx=1时取得最大值a+b=1,
解得 a=4,b=-3,
∴函数y=3-12sinx,
∴其最大值为3+12=15,其最小值为3-12=-9,
周期为2π,
当a<0时,cosx=1时取得最小值a+b=-7,
cosx=-1时取得最大值-a+b=1,
解得 a=-4,b=-3,
∴函数y=3+12sinx,
∴其最大值为3+12=15,其最小值为3-12=-9,
周期为2π.
cosx=1时取得最大值a+b=1,
解得 a=4,b=-3,
∴函数y=3-12sinx,
∴其最大值为3+12=15,其最小值为3-12=-9,
周期为2π,
当a<0时,cosx=1时取得最小值a+b=-7,
cosx=-1时取得最大值-a+b=1,
解得 a=-4,b=-3,
∴函数y=3+12sinx,
∴其最大值为3+12=15,其最小值为3-12=-9,
周期为2π.
点评:本题重点考查了三角函数的图象与性质、函数的最值和周期性等知识点,属于中档题.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
设集合A={x|y=
},B={y|y=2x,x>1},则A∩B为( )
| 3x-x2 |
| A、[0,3] |
| B、(2,3] |
| C、[3,+∞) |
| D、[1,3] |
已知抛物线y2=4x,焦点为P,平面上一定点A(m,0),满足
=2
,过A作直线l,过原点作l的垂线,垂足为Q,则Q的轨迹方程为( )
| OA |
| PA |
| A、y=2x(x≠0) |
| B、x2+y2=1(x≠0) |
| C、(x-1)2+y2=1(y≠0) |
| D、x2-2xy+y2=0(x≠0) |
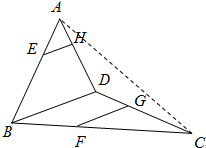 如图,空间四边形ABCD中,E、H为AB、AD的中点,G、F为BC、CD上的点,且
如图,空间四边形ABCD中,E、H为AB、AD的中点,G、F为BC、CD上的点,且