题目内容
4.设AB是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的长轴,若把AB给100等分,过每个分点作AB的垂线,交椭圆的上半部分于P1、P2、…、P99,F1为椭圆的左焦点,则|F1A|+|F1P1|+|F1P2|+…+|F1P99|+|F1B|的值是101a.分析 根据椭圆的定义便可以得到$\sum_{i=1}^{99}(|{F}_{1}{P}_{i}|+|{F}_{2}{P}_{i}|)=2a•99$,而由题意可知P1、P2、…、P99关于y轴对称分布,从而便可得到$\sum_{i=1}^{99}(|{F}_{1}{P}_{i}|)=\frac{1}{2}\sum_{i=1}^{99}(|{F}_{1}{P}_{i}|+|{F}_{2}{P}_{i}|)$,而|F1A|+|F1B|=2a,这样即可得出|F1A|+|F1P1|+|F1P2|+…+|F1P99|+|F1B|的值.
解答 解:由椭圆的定义知|F1Pi|+|F2Pi|=2a(i=1,2,…,99);
∴$\sum_{i=1}^{99}(|{F}_{1}{P}_{i}|+|{F}_{2}{P}_{i}|)=2a•99$;
由题意知P1,P2,…,P99关于y轴成对称分布;
∴$\sum_{i=1}^{99}(|{F}_{1}{P}_{i}|)=\frac{1}{2}\sum_{i=1}^{99}(|{F}_{1}{P}_{i}|+|{F}_{2}{P}_{i}|)=99a$
又∵|F1A|+|F1B|=2a;
故所求的值为101a.
故答案为:101a.
点评 考查椭圆的定义,椭圆的两焦点关于y轴对称,以及椭圆的标准方程,椭圆的长轴的概念,清楚把线段100等分的概念,以及椭圆的对称性.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
6.已知集合A={y|y=|x|+1},B={x|x2≥1},则下列结论正确的是( )
| A. | -3∈A | B. | 3∉B | C. | A∩B=A | D. | A∪B=A |
13.“x>2“是“x2+2x-8>0“成立的( )
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
 已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$离心率为$e=\frac{{\sqrt{3}}}{2}$,以原点为圆心,以椭圆C的短半轴长为半径的圆O与直线l1:$y=x+\sqrt{2}$相切.
已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$离心率为$e=\frac{{\sqrt{3}}}{2}$,以原点为圆心,以椭圆C的短半轴长为半径的圆O与直线l1:$y=x+\sqrt{2}$相切.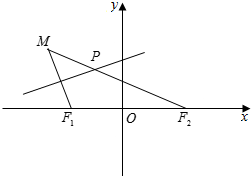 如图所示,点F1(-1,0),F2(1,0),动点M到点F2的距离是$2\sqrt{2}$,线段MF1的中垂线交MF2于点P.
如图所示,点F1(-1,0),F2(1,0),动点M到点F2的距离是$2\sqrt{2}$,线段MF1的中垂线交MF2于点P.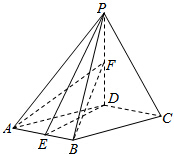 已知四棱锥P-ABCD,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,PD=AD=2,点E为AB中点,点F为PD中点.
已知四棱锥P-ABCD,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,PD=AD=2,点E为AB中点,点F为PD中点.