题目内容
16.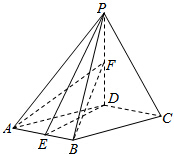 已知四棱锥P-ABCD,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,PD=AD=2,点E为AB中点,点F为PD中点.
已知四棱锥P-ABCD,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,PD=AD=2,点E为AB中点,点F为PD中点.(1)证明平面PED⊥平面PAB;
(2)求二面角P-AB-F的平面角的余弦值.
分析 (1)先由已知条件证明∴△ADB为等边三角形,AB⊥DE,易证AB⊥PD,得到AB⊥面PED,进而证明面PED⊥面PAB.
(2)先由二面角的定义找出二面角的平面角,把二面角的平面角放在一个三角形中,求出此角的余弦值.
解答  (1)证明:连接BD.∵AB=AD,∠DAB=60°,∴△ADB为等边三角形.
(1)证明:连接BD.∵AB=AD,∠DAB=60°,∴△ADB为等边三角形.
∵E是AB中点,∴AB⊥DE.(2分)
∵PD⊥面ABCD,AB?面ABCD,∴AB⊥PD.
∵DE?面PED,PD?面PED,DE∩PD=D,∴AB⊥面PED. (4分)
∵AB?面PAB,
∴面PED⊥面PAB. (6分)
(2)解:∵AB⊥平面PED,PE?面PED,∴AB⊥PE.
连接EF,∵EF?PED,
∴AB⊥EF.
∴∠PEF为二面角P-AB-F的平面角.(9分)
设AD=2,那么PF=FD=1,DE=$\sqrt{3}$.
在△PEF中,PE=$\sqrt{7},EF=2,PF=1$,
∴$cos∠PEF=\frac{{{{(\sqrt{7})}^2}+{2^2}-1}}{{2×2\sqrt{7}}}=\frac{{5\sqrt{7}}}{14}$,
即二面角P-AB-F的平面角的余弦值为$\frac{{5\sqrt{7}}}{14}$.(12分)
点评 本题主要考查面面垂直的判断以及二面角的求解,根据面面垂直的判定定理以及二面角的平面角的定义是解决本题的关键.

练习册系列答案
相关题目
11.设椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左、右焦点分别为F1,F2,离心率为e,过F2的直线与椭圆的交于A,B两点,若△F1AB是以A为顶点的等腰直角三角形,则e2=( )
| A. | 3-2$\sqrt{2}$ | B. | 5-3$\sqrt{2}$ | C. | 9-6$\sqrt{2}$ | D. | 6-4$\sqrt{2}$ |
1.已知点F1,F2为椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左右焦点,若椭圆上存在点P使得$|{\overrightarrow{P{F_1}}}|=2|{\overrightarrow{P{F_2}}}|$,则此椭圆的离心率的取值范围是( )
| A. | (0,$\frac{1}{3}$) | B. | (0,$\frac{1}{2}$] | C. | ($\frac{1}{3}$,$\frac{1}{2}$] | D. | [$\frac{1}{3}$,1) |
8.已知$α∈(\frac{π}{2},π)$,且sin(π+α)=-$\frac{3}{5}$,则tanα=( )
| A. | $-\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{4}$ | D. | $-\frac{4}{3}$ |
 如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,直线F是右准线且准线方程为x=4.A、B分别是其左右顶点,P是椭圆上异于左右顶点的任意一点.直线PA、PB与椭圆的右准线分别交于E、F两点,连接AF与椭圆交于点M.
如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,直线F是右准线且准线方程为x=4.A、B分别是其左右顶点,P是椭圆上异于左右顶点的任意一点.直线PA、PB与椭圆的右准线分别交于E、F两点,连接AF与椭圆交于点M.