题目内容
14.设函数f(x)=|x-4|-|x-1|.(Ⅰ)求不等式f(x)≤1的解集;
(Ⅱ)若{x|f(x)≥t2-2t}∩{x|0≤x≤2}≠∅,求实数t的取值范围.
分析 (Ⅰ)根据绝对值的几何意义求出不等式的解集即可;(Ⅱ)问题转化为f(x)max≥t2-2t在[0,2]成立,求出f(x)的最大值,解出t即可.
解答 解:(Ⅰ)由|x-4|-|x-1|的几何意义知:
f(x)表示点P(x,0)到点A(4,0)和点B(1,0)的距离之差,
故{x|x≥2};
(Ⅱ)使{x|f(x)≥t2-2t}∩{x|0≤x≤2}≠∅成立,
知存在x0∈[0,2]使得f(x0)≥t2-2t成立,
即f(x)max≥t2-2t在[0,2]成立,
f(x)在[0,2]上的最大值是3,
∴t2-2t≤3,解得:-1≤t≤3.
点评 本题考查了绝对值的意义,考查解绝对值不等式问题,是一道中档题,

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.变量x,y满足约束条件$\left\{\begin{array}{l}x+y-2≥0\\ x-y-2≤0\\ y≥1\end{array}\right.$,则目标函数z=x+3y的最小值为( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
4.阅读如图所示的程序框图,运行相应的程序,若判断框内是n≤6,则输出的S为( )
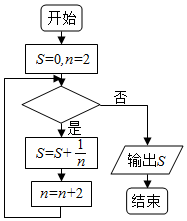

| A. | $\frac{3}{4}$ | B. | $\frac{25}{24}$ | C. | $\frac{11}{12}$ | D. | $\frac{5}{6}$ |
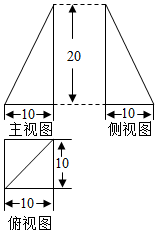 董师傅用铁皮制作一封闭的工件,且三视图如图所示(单位:cm),图中水平线与竖直线垂直),则制作该工件用去的铁皮的面积为(制作过程铁皮的损耗忽略不计)(100(3+$\sqrt{5}$)cm2.
董师傅用铁皮制作一封闭的工件,且三视图如图所示(单位:cm),图中水平线与竖直线垂直),则制作该工件用去的铁皮的面积为(制作过程铁皮的损耗忽略不计)(100(3+$\sqrt{5}$)cm2.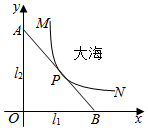 某沿海城市的海边有两条相互垂直的直线型公路l1、l2,海岸边界MPN近似地看成一条曲线段.为开发旅游资源,需修建一条连接两条公路的直线型观光大道AB,且直线AB与曲线MPN有且仅有一个公共点P(即直线与曲线相切),如图所示.若曲线段MPN是函数$y=\frac{a}{x}$图象的一段,点M到l1、l2的距离分别为8千米和1千米,点N到l2的距离为10千米,点P到l2的距离为2千米.以l1、l2分别为x、y轴建立如图所示的平面直角坐标系xOy.
某沿海城市的海边有两条相互垂直的直线型公路l1、l2,海岸边界MPN近似地看成一条曲线段.为开发旅游资源,需修建一条连接两条公路的直线型观光大道AB,且直线AB与曲线MPN有且仅有一个公共点P(即直线与曲线相切),如图所示.若曲线段MPN是函数$y=\frac{a}{x}$图象的一段,点M到l1、l2的距离分别为8千米和1千米,点N到l2的距离为10千米,点P到l2的距离为2千米.以l1、l2分别为x、y轴建立如图所示的平面直角坐标系xOy.