题目内容
6.已知集合A={y|y=|x|+1},B={x|x2≥1},则下列结论正确的是( )| A. | -3∈A | B. | 3∉B | C. | A∩B=A | D. | A∪B=A |
分析 利用不等式的解法分别化简集合A,B,再利用元素与集合的关系、集合与集合的关系即可得出.
解答 解:由y=|x|+1≥1,可得A=[1,+∞).
由x2≥1,解得x≥1,或x≤-1.∴B=(-∞,-1]∪[1,+∞).
∴-3∉A,3∈B,A∩B=A.
故选:C.
点评 本题考查了不等式的解法、元素与集合的关系、集合与集合的关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
17.若函数f(x)=$\sqrt{x-1}$,则函数f(2x)的定义域是( )
| A. | R | B. | [1,+∞) | C. | [0,+∞) | D. | (-∞,0] |
1.已知{an}是等差数列,首项a1>0,a19+a20>0,a19a20<0,则使an>-a1成立的最大自然数n是( )
| A. | 20 | B. | 37 | C. | 38 | D. | 40 |
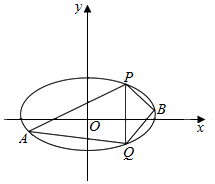 已知椭圆C的中心在原点,焦点在x轴上,离心率等于$\frac{1}{2}$,它的一个短轴端点是(0,2$\sqrt{3}$).
已知椭圆C的中心在原点,焦点在x轴上,离心率等于$\frac{1}{2}$,它的一个短轴端点是(0,2$\sqrt{3}$).