题目内容
19.已知椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为e=$\frac{\sqrt{3}}{2}$,且C1的右焦点与抛物线C2:y2=4$\sqrt{3}$x的焦点相同.(1)求椭圆C1的方程;
(2)求经过点P(-2,0)分别作斜率为k1、k2(k1≠k2)的两条直线,两直线分别与椭圆C1交于M、N两点,当直线MN与y轴垂直时,求k1•k2的值.
分析 (1)由椭圆的离心率和且C1的右焦点与抛物线C2:y2=4$\sqrt{3}$x的焦点相同,列出方程组求出a,b,由此能求出椭圆C1的方程.
(2)设直线PM:y=k1(x+2),与椭圆联立,求出M,同理求出N,由直线MN与y轴垂直,得${k}_{1}+4{k}_{1}{{k}_{2}}^{2}={k}_{2}+4{k}_{2}{{k}_{1}}^{2}$,由此能求出k1k2的值.
解答 解:(1)∵椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为e=$\frac{\sqrt{3}}{2}$,
且C1的右焦点与抛物线C2:y2=4$\sqrt{3}$x的焦点相同,
∴$\left\{\begin{array}{l}{e=\frac{c}{a}=\frac{\sqrt{3}}{2}}\\{c=\sqrt{3}}\end{array}\right.$,解得a=2,c=$\sqrt{3}$,
b2=4-3=1,
∴椭圆C1的方程为$\frac{{x}^{2}}{4}+{y}^{2}=1$.
(2)由题意,当k1=0时,M点的纵坐标为0,直线MN与y轴垂直,则点N的纵坐标也为0,
∴k1=k2=0,与k1≠k2矛盾,∴k1≠0,
设直线PM:y=k1(x+2),
由$\left\{\begin{array}{l}{\frac{{x}^{2}}{4}+{y}^{2}=1}\\{y={k}_{1}(x+2)}\end{array}\right.$,得$(\frac{1}{{{k}_{1}}^{2}}+4){y}^{2}-\frac{4y}{{k}_{1}}=0$,
解得$y=\frac{4{k}_{1}}{1+4{{k}_{1}}^{2}}$或y=0(舍),
∴M($\frac{2-8{{k}_{1}}^{2}}{1+4{{k}_{1}}^{2}}$,$\frac{4{k}_{1}}{1+4{{k}_{1}}^{2}}$),同理N($\frac{2-8{{k}_{2}}^{2}}{1+4{{k}_{2}}^{2}}$,$\frac{4{k}_{2}}{1+4{{k}_{2}}^{2}}$),
∵直线MN与y轴垂直,∴$\frac{4{k}_{1}}{1+4{{k}_{1}}^{2}}$=$\frac{4{k}_{2}}{1+4{{k}_{2}}^{2}}$,
化简,得${k}_{1}+4{k}_{1}{{k}_{2}}^{2}={k}_{2}+4{k}_{2}{{k}_{1}}^{2}$,
∴(k2-k1)(4k1k2-1)=0,
又由k1≠k2,得4k1k2-1=0,
∴k1k2=$\frac{1}{4}$.
点评 本题考查椭圆方程的求法,考查直线的斜率之积的求法,是中档题,解题时要认真审题,注意椭圆性质、直线方程的性质的合理运用.

 阅读快车系列答案
阅读快车系列答案| A. | 20 | B. | 37 | C. | 38 | D. | 40 |
| A. | 3-2$\sqrt{2}$ | B. | 5-3$\sqrt{2}$ | C. | 9-6$\sqrt{2}$ | D. | 6-4$\sqrt{2}$ |
| A. | $-\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{4}$ | D. | $-\frac{4}{3}$ |
 如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,直线F是右准线且准线方程为x=4.A、B分别是其左右顶点,P是椭圆上异于左右顶点的任意一点.直线PA、PB与椭圆的右准线分别交于E、F两点,连接AF与椭圆交于点M.
如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,直线F是右准线且准线方程为x=4.A、B分别是其左右顶点,P是椭圆上异于左右顶点的任意一点.直线PA、PB与椭圆的右准线分别交于E、F两点,连接AF与椭圆交于点M.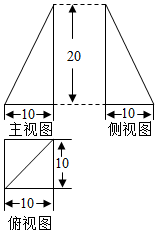 董师傅用铁皮制作一封闭的工件,且三视图如图所示(单位:cm),图中水平线与竖直线垂直),则制作该工件用去的铁皮的面积为(制作过程铁皮的损耗忽略不计)(100(3+$\sqrt{5}$)cm2.
董师傅用铁皮制作一封闭的工件,且三视图如图所示(单位:cm),图中水平线与竖直线垂直),则制作该工件用去的铁皮的面积为(制作过程铁皮的损耗忽略不计)(100(3+$\sqrt{5}$)cm2.