题目内容
13.“x>2“是“x2+2x-8>0“成立的( )| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 由x2+2x-8>0解得x>2,或x<-4.即可判断出结论.
解答 解:由x2+2x-8>0解得x>2,或x<-4.
∴“x>2“是“x2+2x-8>0“成立的充分不必要条件.
故选:B.
点评 本题考查了不等式的解法、简易逻辑的判定方法,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
1.已知点F1,F2为椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左右焦点,若椭圆上存在点P使得$|{\overrightarrow{P{F_1}}}|=2|{\overrightarrow{P{F_2}}}|$,则此椭圆的离心率的取值范围是( )
| A. | (0,$\frac{1}{3}$) | B. | (0,$\frac{1}{2}$] | C. | ($\frac{1}{3}$,$\frac{1}{2}$] | D. | [$\frac{1}{3}$,1) |
8.已知$α∈(\frac{π}{2},π)$,且sin(π+α)=-$\frac{3}{5}$,则tanα=( )
| A. | $-\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{4}$ | D. | $-\frac{4}{3}$ |
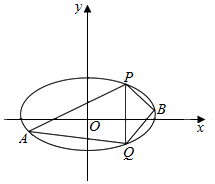 已知椭圆C的中心在原点,焦点在x轴上,离心率等于$\frac{1}{2}$,它的一个短轴端点是(0,2$\sqrt{3}$).
已知椭圆C的中心在原点,焦点在x轴上,离心率等于$\frac{1}{2}$,它的一个短轴端点是(0,2$\sqrt{3}$).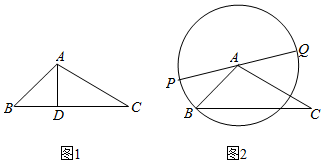 在△ABC中.
在△ABC中.