题目内容
星期天,刘先生到电信局打算上网开户,经询问,记录了可能需要的三种方式所花费的费用资料,现将资料整理如下:
①163普通:上网资费2元/小时;
②163A:每月50元(可上网50小时),超过50小时的部分资费2元/小时;
③ADSLD:每月70元,时长不限(其他因素忽略不计).
请你用所学的函数知识对上网方式与费用问题作出研究:
(1)分别写出三种上网方式中所用资费与时间的函数解析式;
(2)在同一坐标系内分别画出三种方式所需资费与时间的函数图象;
(3)根据你的研究,请给刘先生一个合理化的建议.
①163普通:上网资费2元/小时;
②163A:每月50元(可上网50小时),超过50小时的部分资费2元/小时;
③ADSLD:每月70元,时长不限(其他因素忽略不计).
请你用所学的函数知识对上网方式与费用问题作出研究:
(1)分别写出三种上网方式中所用资费与时间的函数解析式;
(2)在同一坐标系内分别画出三种方式所需资费与时间的函数图象;
(3)根据你的研究,请给刘先生一个合理化的建议.
考点:分段函数的解析式求法及其图象的作法
专题:函数的性质及应用
分析:(1)有三种消费方式,①是一次函数,②有两种要求则为分段函数,③是常函数,分别列出解析式及取值范围即可;每月按30天计算.
(2)因为都为线性函数,作图时可任取两点作出;
(3)通过第二问图分析,提出建议.
(2)因为都为线性函数,作图时可任取两点作出;
(3)通过第二问图分析,提出建议.
解答:
解:(1)①y=2x,(0≤x≤720)
②y=
③y=70(0≤x≤720);
(2)如图所示;

(3)每月0--25小时,选方案①;
每月25--60小时,选方案②;
每月60小时以上,选方案③
②y=
|
③y=70(0≤x≤720);
(2)如图所示;

(3)每月0--25小时,选方案①;
每月25--60小时,选方案②;
每月60小时以上,选方案③
点评:本题是一个收费问题提供了三种方案,所以要分别建立模型,再写成分段函数,再研究图象,要结合用户的用时情况提出建议.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数y=
在第二象限内单调递增,则m的最大负整数是( )
| 1 |
| x1-m |
| A、-4 | B、-3 | C、-2 | D、-1 |
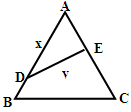 如图,公园有一块边长为2的等边的三角地,现修成草坪,图中DE把草坪分成面积相等的两部分,D在AB上,E在AC上.设AD=x(x≥0),DE=y,求用x表示y的函数关系式,并求函数的定义域.
如图,公园有一块边长为2的等边的三角地,现修成草坪,图中DE把草坪分成面积相等的两部分,D在AB上,E在AC上.设AD=x(x≥0),DE=y,求用x表示y的函数关系式,并求函数的定义域.