题目内容
有四个关于三角函数的命题:
p1:?x∈R,使得sinx+cosx=
;
p2:?x,y∈R,使得sin(x+y)=sinx+siny;
p3:?x∈[0,π],都有
=sinx;
p4:任意锐角△ABC中,恒有sinA>cosB成立;
其中真命题的个数是( )
p1:?x∈R,使得sinx+cosx=
| 3 |
| 2 |
p2:?x,y∈R,使得sin(x+y)=sinx+siny;
p3:?x∈[0,π],都有
|
p4:任意锐角△ABC中,恒有sinA>cosB成立;
其中真命题的个数是( )
| A、1 | B、2 | C、3 | D、4 |
考点:命题的真假判断与应用
专题:三角函数的图像与性质
分析:p1:利用三角恒等变换及正弦函数的值域可得sinx+cosx=
sin(x+
)≤
,从而可判断p1错误;
p2::?x=0,y=0∈R,使得sin(0+0)=sin0+sin0,可判断p2正确;
p3:利用正弦函数的图象与性质可知x∈[0,π]时,sinx≥0,再利用降幂公式可判断p3正确;
p4:利用诱导公式及正弦函数的单调性质可判断p4正确.
| 2 |
| π |
| 4 |
| 2 |
p2::?x=0,y=0∈R,使得sin(0+0)=sin0+sin0,可判断p2正确;
p3:利用正弦函数的图象与性质可知x∈[0,π]时,sinx≥0,再利用降幂公式可判断p3正确;
p4:利用诱导公式及正弦函数的单调性质可判断p4正确.
解答:
解:p1:∵sinx+cosx=
sin(x+
)≤
,故不存在x∈R,使得sinx+cosx=
,即p1错误;
p2:?x=0,y=0∈R,使得sin(0+0)=sin0+sin0,故p2正确;
p3:∵x∈[0,π]时,sinx≥0,故当x∈[0,π]时,
=|sinx|=sinx,即p3正确;
p4:锐角△ABC中,A+B>
,
>A>
-B>0,
恒有sinA>sin(
-B)=cosB成立,即p4正确;
综上所述,真命题的个数是3个,
故选:C.
| 2 |
| π |
| 4 |
| 2 |
| 3 |
| 2 |
p2:?x=0,y=0∈R,使得sin(0+0)=sin0+sin0,故p2正确;
p3:∵x∈[0,π]时,sinx≥0,故当x∈[0,π]时,
|
p4:锐角△ABC中,A+B>
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
恒有sinA>sin(
| π |
| 2 |
综上所述,真命题的个数是3个,
故选:C.
点评:本题考查命题的真假判断与应用,着重考查三角函数的诱导公式、辅助角公式及降幂公式的应用,属于中档题.

练习册系列答案
相关题目
 若某三棱柱截去一个三棱锥后所剩几何体的三视图如图所示,则此几何体的体积等于( )
若某三棱柱截去一个三棱锥后所剩几何体的三视图如图所示,则此几何体的体积等于( )| A、30 | B、12 | C、24 | D、4 |
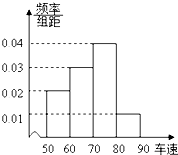 某雷达测速区规定:凡车速大于或等于80km/h的汽车视为“超速”,并将受到处罚.如图是某路段的一个检测点对200辆汽车的车速进行检测所得结果的频率分布直方图,则从图中可以看出被处罚的汽车大约有( )
某雷达测速区规定:凡车速大于或等于80km/h的汽车视为“超速”,并将受到处罚.如图是某路段的一个检测点对200辆汽车的车速进行检测所得结果的频率分布直方图,则从图中可以看出被处罚的汽车大约有( )| A、20辆 | B、40辆 |
| C、60辆 | D、80辆 |
 一个长、宽分别为
一个长、宽分别为| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、π |
若集合M={y|y=3x},集合S={x|y=lg(x-1)},则下列各式正确的是( )
| A、M∪S=M | B、M∪S=S |
| C、M=S | D、M∩S=∅ |
下列函数中,既是奇函数又在[-1,1]上是单调递减的函数是( )
| A、f(x)=sinx | ||
| B、f(x)=-|x-1| | ||
C、f(x)=
| ||
D、f(x)=ln
|
 如图,在y轴的正半轴上依次有点A1、A2、…、An,其中点A1(0,1)、A2(0,10),且|An-1An|=3|AnAn+1|(n=2,3,4,…),在射线y=x(x≥0)上依次有点B1、B2、…、Bn,点B1的坐标为(3,3),且|OBn|=|OBn-1|+2
如图,在y轴的正半轴上依次有点A1、A2、…、An,其中点A1(0,1)、A2(0,10),且|An-1An|=3|AnAn+1|(n=2,3,4,…),在射线y=x(x≥0)上依次有点B1、B2、…、Bn,点B1的坐标为(3,3),且|OBn|=|OBn-1|+2