题目内容
已知函数f(x)=sin2x+
sinxsin(x+
)
(Ⅰ)求f(x)的最小正周期T;
(Ⅱ)求函数f(x)的单调递增区间;
(Ⅲ)求函数f(x)在区间[0,
]上的取值范围.
| 3 |
| π |
| 2 |
(Ⅰ)求f(x)的最小正周期T;
(Ⅱ)求函数f(x)的单调递增区间;
(Ⅲ)求函数f(x)在区间[0,
| 2π |
| 3 |
考点:三角函数中的恒等变换应用,正弦函数的图象
专题:三角函数的图像与性质
分析:(Ⅰ)由三角函数公式化简可得f(x)=sin(2x-
)+
,可得周期T=
=π;(Ⅱ)由-
+2kπ≤2x-
≤
+2kπ解不等式可得单调递增区间;(Ⅲ)由x∈[0,
]可得2x-
∈[-
,
π],进而可得sin(2x-
)∈[-
,1],可得f(x)∈[0,
].
| π |
| 6 |
| 1 |
| 2 |
| 2π |
| 2 |
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
| 2π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| 7 |
| 6 |
| π |
| 6 |
| 1 |
| 2 |
| 3 |
| 2 |
解答:
解:(Ⅰ)化简可得f(x)=sin2x+
sinxsin(x+
)
=
+
sinxcosx=
sin2x-
cos2x+
=sin(2x-
)+
,可得周期T=
=π;
(Ⅱ)由-
+2kπ≤2x-
≤
+2kπ得-
+kπ≤x≤
+kπ,k∈z
∴函数f(x)的单调递增区间是[-
+kπ,
+kπ],k∈z;
(Ⅲ)由x∈[0,
]可得2x-
∈[-
,
π],
∴sin(2x-
)∈[-
,1],∴f(x)∈[0,
],
∴函数f(x)在区间[0,
]上的取值范围为[0,
].
| 3 |
| π |
| 2 |
=
| 1-cos2x |
| 2 |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=sin(2x-
| π |
| 6 |
| 1 |
| 2 |
| 2π |
| 2 |
(Ⅱ)由-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
| π |
| 3 |
∴函数f(x)的单调递增区间是[-
| π |
| 6 |
| π |
| 3 |
(Ⅲ)由x∈[0,
| 2π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| 7 |
| 6 |
∴sin(2x-
| π |
| 6 |
| 1 |
| 2 |
| 3 |
| 2 |
∴函数f(x)在区间[0,
| 2π |
| 3 |
| 3 |
| 2 |
点评:本题考查三角函数恒等变换,涉及三角函数的单调性和最值,属基础题.

练习册系列答案
相关题目
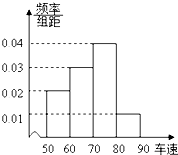 某雷达测速区规定:凡车速大于或等于80km/h的汽车视为“超速”,并将受到处罚.如图是某路段的一个检测点对200辆汽车的车速进行检测所得结果的频率分布直方图,则从图中可以看出被处罚的汽车大约有( )
某雷达测速区规定:凡车速大于或等于80km/h的汽车视为“超速”,并将受到处罚.如图是某路段的一个检测点对200辆汽车的车速进行检测所得结果的频率分布直方图,则从图中可以看出被处罚的汽车大约有( )