题目内容
若a=n2+1，n∈N，A={x|x=k2-4k+5，k∈N}，则a与A的关系是 ．
考点：元素与集合关系的判断
专题：计算题,集合
分析：验证a满足集合A的共同特征．
解答：
解：∵x=k2-4k+5=（k-2）2+1，k∈N，
∴a=n2+1满足x=k2-4k+5=（k-2）2+1，k∈N，的特征；
∴a∈A．
故答案为：a∈A．
∴a=n2+1满足x=k2-4k+5=（k-2）2+1，k∈N，的特征；
∴a∈A．
故答案为：a∈A．
点评：本题考查了元素与集合的关系判断．
练习册系列答案
名校课堂系列答案
相关题目
某几何体的三视图如图所示，则该几何体是（ ）
| A、圆柱 | B、圆锥 |
| C、三棱柱 | D、三棱锥 |
如图，在y轴的正半轴上依次有点A1、A2、…、An，其中点A1（0，1）、A2（0，10），且|An-1An|=3|AnAn+1|（n=2，3，4，…），在射线y=x（x≥0）上依次有点B1、B2、…、Bn，点B1的坐标为（3，3），且|OBn|=|OBn-1|+2
若某三棱柱截去一个三棱锥后所剩几何体的三视图如图所示，则此几何体的体积等于（ ）| A、30 | B、12 | C、24 | D、4 |
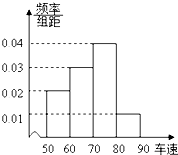某雷达测速区规定：凡车速大于或等于80km/h的汽车视为“超速”，并将受到处罚．如图是某路段的一个检测点对200辆汽车的车速进行检测所得结果的频率分布直方图，则从图中可以看出被处罚的汽车大约有（ ）