题目内容
命题p:“?x∈(0,有9x+
≥7a+1,其中常数a<0”,若命题q:“?x0∈R,x02+2ax0+2-a=0,若“p且q”为假命题,“p或q”为真命题,求实数a的取值范围.
| a2 |
| x |
考点:复合命题的真假
专题:简易逻辑
分析:首先,分别判断两个命题为真命题时,a的取值范围,然后,结合“p且q”为假命题,“p或q”为真命题,则命题p和命题q一真一假,分情况进行讨论完成结果.
解答:
解:若p为真命题,则
(9x+
)min≥7a+1,
又∵9x+
≥2
=6|a|=-6a,
∴-6a≥7a+1,
∴a≤-
,
若q 为真命题,则方程x2+2ax+2-a=0有实根,
∴△=4a2-4(2-a)≥0,
∴a≤-2或a≥1,
若“p且q”为假命题,“p或q”为真命题,
则命题p和命题q一真一假,
∴当p真q假时,则
,
∴-2<a≤-
,
当p假q真时,则
,
∴a≥1,
综上,符合条件的a的取值范围为(-2,-
]∪[1,+∞).
(9x+
| a2 |
| x |
又∵9x+
| a2 |
| x |
9x•
|
∴-6a≥7a+1,
∴a≤-
| 1 |
| 13 |
若q 为真命题,则方程x2+2ax+2-a=0有实根,
∴△=4a2-4(2-a)≥0,
∴a≤-2或a≥1,
若“p且q”为假命题,“p或q”为真命题,
则命题p和命题q一真一假,
∴当p真q假时,则
|
∴-2<a≤-
| 1 |
| 13 |
当p假q真时,则
|
∴a≥1,
综上,符合条件的a的取值范围为(-2,-
| 1 |
| 13 |
点评:本题重点考查了命题的真假判断、复合命题的真假判断等知识,属于中档题,解题关键是准确判断符合命题的真假情形.

练习册系列答案
相关题目
如果命题“¬P”为假,命题“P∧q”为假,那么则有( )
| A、q为真 |
| B、p∨q为假 |
| C、p∨q为真 |
| D、(¬p)∧(¬q)为真 |
下列函数中,是奇函数,又在定义域内为减函数的是( )
A、y=(
| ||
B、y=
| ||
| C、y=-x3 | ||
| D、y=x2 |
已知{an}是递增的等比数列a2=2,a4-
a3=-2,则此数列的公比q为( )
| 5 |
| 2 |
| A、3 | ||
| B、4 | ||
C、
| ||
| D、2 |
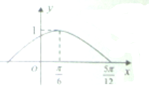 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,-
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,-