题目内容
已知函数f(x)=
(x≠0)是奇函数,且满足f(1)=f(4)
(1)求实数a,b的值;
(2)试指出函数的单调区间(不必证明),并用定义法证明函数f(x)在区间(0,2]的单调性;
(3)是否存在实数k同时满足以下两个条件:
①不等式f(x)+
>0对x∈(0,+∞)恒成立;
②方程f(x)=k在x∈[-6,-1]上有解.若存在,试求出实数k的取值范围,若不存在,请说明理由.
| x2+ax+b |
| x |
(1)求实数a,b的值;
(2)试指出函数的单调区间(不必证明),并用定义法证明函数f(x)在区间(0,2]的单调性;
(3)是否存在实数k同时满足以下两个条件:
①不等式f(x)+
| k |
| 2 |
②方程f(x)=k在x∈[-6,-1]上有解.若存在,试求出实数k的取值范围,若不存在,请说明理由.
考点:函数最值的应用,函数单调性的性质,函数奇偶性的判断
专题:综合题,函数的性质及应用
分析:(1)利用f(1)=f(4),求出b的值,利用f(x)=
(x≠0)是奇函数,求出a的值;
(2)根据函数单调性的定义证明即可;
(3)分别求出满足两个条件的实数k的取值范围,即可得出结论.
| x2+ax+b |
| x |
(2)根据函数单调性的定义证明即可;
(3)分别求出满足两个条件的实数k的取值范围,即可得出结论.
解答:
解:(1)由f(1)=f(4)得1+a+b=
,解得b=4,(2分)
由f(x)=
(x≠0)是奇函数,得
+
=0,
∴2a=0,
∴a=0; (5分)
(2)由(1)知,f(x)=x+
,任取x1,x2∈(0,2],且x1<x2,
f(x1)-f(x2)=(x1-x2)•
,
∵x1,x2∈(0,2],且x1<x2,
∴x1-x2<0,
<0,
∴f(x1)-f(x2)>0,
∴f(x1)>f(x2),(8分)
∴函数f(x)在区间(0,2]单调递减; (9分)
类似地,可证f(x)在区间(2,+∞)单调递增.
(3)对于条件①:
由(2)可知函数f(x)在x∈(0,+∞)上有最小值f(2)=4 (10分)
故若f(x)+
>0对x∈(0,+∞)恒成立,
则需4>-
,∴k>-8; (11分)
对于条件②:由(2)可知函数f(x)在(-∞,-2)单调递增,
在[-2,0)单调递减,
∴函数f(x)在[-6,-2]单调递增,在[-2,-1]单调递减,(12分)
又f(-6)=-
,f(-2)=-4,f(-1)=-5,
∴函数f(x)在[-6,-1]上的值域为[-
,-4],(13分)
若方程f(x)=k在[-6,-1]有解,则需-
≤k≤-4,
若同时满足条件①②,则需-
≤k≤-4.
故当-
≤k≤-4时,条件①②同时满足. (15分)
| 16+4a+b |
| 4 |
由f(x)=
| x2+ax+b |
| x |
| x2-ax+b |
| -x |
| x2+ax+b |
| x |
∴2a=0,
∴a=0; (5分)
(2)由(1)知,f(x)=x+
| 4 |
| x |
f(x1)-f(x2)=(x1-x2)•
| x1x2-4 |
| x1x2 |
∵x1,x2∈(0,2],且x1<x2,
∴x1-x2<0,
| x1x2-4 |
| x1x2 |
∴f(x1)-f(x2)>0,
∴f(x1)>f(x2),(8分)
∴函数f(x)在区间(0,2]单调递减; (9分)
类似地,可证f(x)在区间(2,+∞)单调递增.
(3)对于条件①:
由(2)可知函数f(x)在x∈(0,+∞)上有最小值f(2)=4 (10分)
故若f(x)+
| k |
| 2 |
则需4>-
| k |
| 2 |
对于条件②:由(2)可知函数f(x)在(-∞,-2)单调递增,
在[-2,0)单调递减,
∴函数f(x)在[-6,-2]单调递增,在[-2,-1]单调递减,(12分)
又f(-6)=-
| 20 |
| 3 |
∴函数f(x)在[-6,-1]上的值域为[-
| 20 |
| 3 |
若方程f(x)=k在[-6,-1]有解,则需-
| 20 |
| 3 |
若同时满足条件①②,则需-
| 20 |
| 3 |
故当-
| 20 |
| 3 |
点评:本题考查函数的性质,考查函数的单调性与值域,考查学生分析解决问题的能力,难度中等.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
已知点F(-c,0)(c>0)是双曲线
-
=1的左焦点,离心率为e,过F且平行于双曲线渐近线的直线与圆x2+y2=c2交于点P,且点P在抛物线y2=3cx上,则e2=( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
点P(x,y)在直线x+y-2=0上,则P到原点距离的最小值是( )
A、2
| ||
B、
| ||
| C、1 | ||
| D、2. |
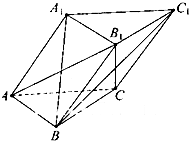 已知三棱柱ABC-A1B1C1中,底面边长和侧棱长均为a,侧面A1ACC1⊥底面ABC,A1B=
已知三棱柱ABC-A1B1C1中,底面边长和侧棱长均为a,侧面A1ACC1⊥底面ABC,A1B=