题目内容
在m(m≥2,m∈N+)个不同数的排列(P1,P2,…,Pm)中,若1≤i<j≤m时,Pi>Pj(即前面某数大于
后面某数)则称Pi与Pj构成一个逆序,一个排列的全部逆序的总数称为该排列的逆序数,例如排列(2,40,3,1)中有逆序“2与1”,“40与3”,“40与1”,“3与1”其逆序数等于4.
(1)求(1,3,40,2)的逆序数;
(2)已知n+2(n∈N+)个不同数的排列(P1,P2,…,Pn+1,Pn+2)的逆序数是2.
(ⅰ)求(Pn+2,Pn+1,…,P2,P1)的逆序数an
(ⅱ)令bn=
+
,证明2n+
≤b1+b2+…+bn<2n+
.
后面某数)则称Pi与Pj构成一个逆序,一个排列的全部逆序的总数称为该排列的逆序数,例如排列(2,40,3,1)中有逆序“2与1”,“40与3”,“40与1”,“3与1”其逆序数等于4.
(1)求(1,3,40,2)的逆序数;
(2)已知n+2(n∈N+)个不同数的排列(P1,P2,…,Pn+1,Pn+2)的逆序数是2.
(ⅰ)求(Pn+2,Pn+1,…,P2,P1)的逆序数an
(ⅱ)令bn=
| an+2 |
| an+1+2 |
| an+1+2 |
| an+2 |
| 1 |
| 2 |
| 5 |
| 3 |
考点:数列的求和
专题:等差数列与等比数列
分析:(1)(1,3,40,2)中逆序数有2个.
(2)(ⅰ)n+1数中任取两个比较大小,共有
个大小关系,由此能求出结果.
(ⅱ)bn=
+
=2+
-
,从而得到b1+b2+…+bn=2n+1+
-
-
.由此能证明2n+
≤b1+b2+…+bn<2n+
.
(2)(ⅰ)n+1数中任取两个比较大小,共有
| C | 2 n+2 |
(ⅱ)bn=
| an+2 |
| an+1+2 |
| an+1+2 |
| an+2 |
| 2 |
| n+1 |
| 2 |
| n-3 |
| 2 |
| 3 |
| 2 |
| n+2 |
| 2 |
| n+3 |
| 1 |
| 2 |
| 5 |
| 3 |
解答:
解:(1)(1,3,40,2)有逆序“3,2”,“40,2”,其逆序数有2个.
(2)(ⅰ)n+1数中任取两个比较大小,
共有
个大小关系,
∴an
-2,n∈N*.
(ii)bn=
+
=
+
=
+
=2+
-
,
∴b1+b2+…+bn=2n+
-
=2n+1+
-
-
.
∵y=-
-
单调递增,
∴-
-
≤-
-
<0,
∴2n+
≤b1+b2+…+bn<2n+
.
(2)(ⅰ)n+1数中任取两个比较大小,
共有
| C | 2 n+2 |
∴an
| =C | 2 n+2 |
(ii)bn=
| an+2 |
| an+1+2 |
| an+1+2 |
| an+2 |
=
| ||
|
| ||
|
=
| n+1 |
| n+3 |
| n+3 |
| n+1 |
=2+
| 2 |
| n+1 |
| 2 |
| n-3 |
∴b1+b2+…+bn=2n+
| n |
 |
| i=1 |
| 2 |
| i+1 |
| n |
 |
| i=1 |
| 2 |
| i+3 |
=2n+1+
| 2 |
| 3 |
| 2 |
| n+2 |
| 2 |
| n+3 |
∵y=-
| 2 |
| n+2 |
| 2 |
| n+3 |
∴-
| 2 |
| 3 |
| 1 |
| 2 |
| 2 |
| n+2 |
| 2 |
| n+3 |
∴2n+
| 1 |
| 2 |
| 5 |
| 3 |
点评:本题考查逆序数的求法,考查不等式的证明,解题时要认真审题,注意裂项求和法的合理运用,注意函数单调性的灵活运用.

练习册系列答案
相关题目
如果θ=3rad,那么角θ的终边所在的象限是( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
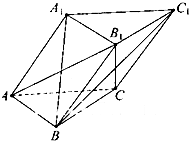 已知三棱柱ABC-A1B1C1中,底面边长和侧棱长均为a,侧面A1ACC1⊥底面ABC,A1B=
已知三棱柱ABC-A1B1C1中,底面边长和侧棱长均为a,侧面A1ACC1⊥底面ABC,A1B=