题目内容
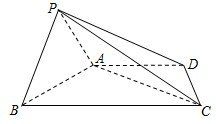 如图,四棱锥P-ABCD中,底面ABCD为梯形,AD∥BC,AB=AD=
如图,四棱锥P-ABCD中,底面ABCD为梯形,AD∥BC,AB=AD=| 1 |
| 2 |
(Ⅰ)求证:BC∥平面PAD;
(Ⅱ)求证:PB⊥AC;
(Ⅲ)是否存在点Q,到四棱锥P-ABCD各顶点的距离都相等?并说明理由.
考点:直线与平面平行的判定,直线与平面垂直的判定,点、线、面间的距离计算
专题:空间位置关系与距离
分析:(Ⅰ)根据底面ABCD为梯形,推断出AD∥BC,进而利用线面平行的判定定理推断出 BC∥平面PAD.
(Ⅱ)设BC的中点为O,连结AO,在梯形ABCD中,根据AB=AD=
BC,∠ABC=60°,推断出△ABO为等边三角形,又 AD∥BC,推断出四边形OCDA为菱形.由∠AOC=120°,OA=OC,求得∠OAC,进而求得∠BAC=90°,判断出AB⊥AC,根据平面PAB⊥平面ABCD,AB是交线,推断出AC⊥平面PAB,进而根据线面垂直的性质推断出PB⊥AC.
(Ⅲ)PA⊥PB,PB⊥AC根据线面垂直的判定定理推断出PB⊥平面PAC进而可知PB⊥PC,推断出△PBC为直角三角形,连结BD,证明出△ABC≌△DCB,推断出△DBC为直角三角形,推断出点O是三个直角三角形:△PBC、△ABC和△DBC的共同的斜边BC的中点,进而可知 OA=OB=OC=OD=OP,进而可知存在点Q(即点O)到四棱锥P-ABCD各顶点的距离都相等.
(Ⅱ)设BC的中点为O,连结AO,在梯形ABCD中,根据AB=AD=
| 1 |
| 2 |
(Ⅲ)PA⊥PB,PB⊥AC根据线面垂直的判定定理推断出PB⊥平面PAC进而可知PB⊥PC,推断出△PBC为直角三角形,连结BD,证明出△ABC≌△DCB,推断出△DBC为直角三角形,推断出点O是三个直角三角形:△PBC、△ABC和△DBC的共同的斜边BC的中点,进而可知 OA=OB=OC=OD=OP,进而可知存在点Q(即点O)到四棱锥P-ABCD各顶点的距离都相等.
解答:
(Ⅰ)证明:底面ABCD为梯形,AD∥BC,
又 BC?平面PAD,AD?平面PAD,
所以 BC∥平面PAD.
(Ⅱ)证明:设BC的中点为O,连结AO,在梯形ABCD中,
因为 AB=AD=
BC,∠ABC=60°,
所以△ABO为等边三角形,OA=1,
又 AD∥BC,
所以 四边形OCDA为菱形.
因为∠AOC=120°,OA=OC,
所以∠OAC=30°,
所以∠BAC=90°,AB⊥AC,
又平面PAB⊥平面ABCD,AB是交线,
所以 AC⊥平面PAB,
所以 AC⊥PB,即PB⊥AC.
(Ⅲ)解:因为 PA⊥PB,PB⊥AC,所以PB⊥平面PAC.
所以,PB⊥PC,
所以△PBC为直角三角形,∠BPC=90°.
连结BD,由(Ⅱ)知∠BCD=60°,
所以△ABC≌△DCB,
所以△DBC为直角三角形,∠BDC=90°.
所以点O是三个直角三角形:△PBC、△ABC和△DBC的共同的斜边BC的中点,
所以 OA=OB=OC=OD=OP,
所以存在点Q(即点O)到四棱锥P-ABCD各顶点的距离都相等.
又 BC?平面PAD,AD?平面PAD,
所以 BC∥平面PAD.
(Ⅱ)证明:设BC的中点为O,连结AO,在梯形ABCD中,
因为 AB=AD=
| 1 |
| 2 |
所以△ABO为等边三角形,OA=1,
又 AD∥BC,
所以 四边形OCDA为菱形.
因为∠AOC=120°,OA=OC,
所以∠OAC=30°,
所以∠BAC=90°,AB⊥AC,
又平面PAB⊥平面ABCD,AB是交线,
所以 AC⊥平面PAB,
所以 AC⊥PB,即PB⊥AC.
(Ⅲ)解:因为 PA⊥PB,PB⊥AC,所以PB⊥平面PAC.
所以,PB⊥PC,
所以△PBC为直角三角形,∠BPC=90°.
连结BD,由(Ⅱ)知∠BCD=60°,
所以△ABC≌△DCB,
所以△DBC为直角三角形,∠BDC=90°.
所以点O是三个直角三角形:△PBC、△ABC和△DBC的共同的斜边BC的中点,
所以 OA=OB=OC=OD=OP,
所以存在点Q(即点O)到四棱锥P-ABCD各顶点的距离都相等.
点评:本题主要考查了线面平行和线面垂直的判定定理及性质.考查了学生对基础知识的综合运用.

练习册系列答案
相关题目
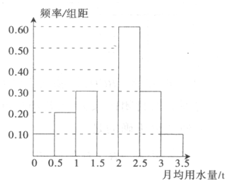 我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市为了节约生活用水,计划在本市试行居民生活用水定额管理(即确定一个居民月均用水量标准?用水量不超过a的部分按照平价收费,超过a的部分按照议价收费).为了较为合理地确定出这个标准,通过抽样获得了 100位居民某年的月均用水量(单位:t),制作了频率分布直方图,
我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市为了节约生活用水,计划在本市试行居民生活用水定额管理(即确定一个居民月均用水量标准?用水量不超过a的部分按照平价收费,超过a的部分按照议价收费).为了较为合理地确定出这个标准,通过抽样获得了 100位居民某年的月均用水量(单位:t),制作了频率分布直方图,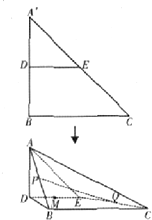 如图,在Rt△A′BC中,A′B=BC=2,D,E分别是A′B,A′C的中点,将△A′DE沿线段DE折起到△ADE,使平面ADE⊥平面DBCE.
如图,在Rt△A′BC中,A′B=BC=2,D,E分别是A′B,A′C的中点,将△A′DE沿线段DE折起到△ADE,使平面ADE⊥平面DBCE. 过x轴上动点A(a,0),引抛物线y=x2+3的两条切线AP、AQ,切点分别为P、Q.
过x轴上动点A(a,0),引抛物线y=x2+3的两条切线AP、AQ,切点分别为P、Q.