甲.乙两袋装有大小相同的红球和白球.甲袋装有2个红球.2个白球,乙袋装有2个红球.n个白球．从甲.乙两袋中各任取一个球．(1)若n=3.求取到的2个球全是红球的概率,(2)若取到的2个球中至少有1个为红球的概率是58.求n的值．题目和参考答案——青夏教育精英家教网—

题目内容

甲、乙两袋装有大小相同的红球和白球，甲袋装有2个红球，2个白球；乙袋装有2个红球，n个白球．从甲，乙两袋中各任取一个球．
（1）若n=3，求取到的2个球全是红球的概率；
（2）若取到的2个球中至少有1个为红球的概率是

，求n的值．

考点：相互独立事件的概率乘法公式,n次独立重复试验中恰好发生k次的概率

专题：概率与统计

分析：（1）n=3时，所有的取法共有4×5种，其中，取到的2个球全是红球的取法有2×2种，由此求得取到的2个球全是红球的概率．
（2）根据取到的2个球中没有红球的概率为

4(2+n)

，可得取到的2个球中至少有1个为红球的概率是 p=1-

4(2+n)

，由此解得n的值．

解答： 解：（1）∵n=3，∴所有的取法共有4×5=20种，其中，取到的2个球全是红球的取法有2×2=4种，
则取到的2个球全是红球的概率p=

．
（2）∵若取到的2个球中没有红球的概率为

4(2+n)

，
∴取到的2个球中至少有1个为红球的概率是 p=1-

4(2+n)

，
解得n=6．

点评：本题主要考查相互独立事件的概率乘法公式，所求的事件的概率与它的对立事件的概率之间的关系，属于中档题．

练习册系列答案

A	85	80	85	60	90
B	70	x	95	y	75

由于表格被污损，数据x看不清，统计员只记得A、B两种出租车的氮氧化物排放量的平均值相等，且方差分别记为s_A²，s_B²．
（1）求x及s_B²的值；
（2）从被检测的6辆B种型号的出租车中任取3辆，记“氮氧化物排放量未超过80mg/km”的车辆数为ξ，求ξ的分布列和数学期望．

若α，β为两个不同的平面，m、n为不同直线，下列推理：
①若α⊥β，m⊥α，n⊥β，则直线m⊥n；
②若直线m∥平面α，直线n⊥直线m，则直线n⊥平面α；
③若直线m∥n，m⊥α，n?β，则平面α⊥平面β；
④若平面α∥平面β，直线m⊥平面β，n?α，则直线m⊥直线n；
其中正确说法的序号是

．

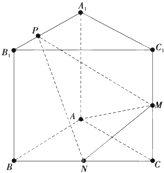如图，已知三棱柱ABC-A₁B₁C₁的侧棱与底面垂直，AA₁=AB=AC=1，AB⊥AC，M、N分别是CC₁，BC的中点，点P在线段A₁B₁上，且

A1P

=λ

A 1B1

（1）证明：无论λ取何值，总有AM⊥PN；
（2）当λ=

时，求直线PN与平面ABC所成角的余弦值．

我校高2014级迎新晚会的舞台天花板上有前、后两排共4个灯架，每排2个，每个灯架上安装了5盏射灯，每盏射灯发光的概率为

．若一个灯架上至少有3盏射灯正常发光，则这个灯架不需要维修，否则需要维修．
（Ⅰ）求恰有两个灯架需要维修的概率；
（Ⅱ）若前排每个灯架的维修费用为100元，后排每个灯架的维修费用为200元，记ξ为维修灯架的总费用，求随机变量ξ的分布列及数学期望．

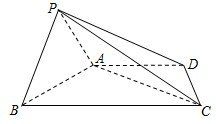如图，四棱锥P-ABCD中，底面ABCD为梯形，AD∥BC，AB=AD=

BC，∠ABC=60°，平面PAB⊥平面ABCD，PA⊥PB．
（Ⅰ）求证：BC∥平面PAD；
（Ⅱ）求证：PB⊥AC；
（Ⅲ）是否存在点Q，到四棱锥P-ABCD各顶点的距离都相等？并说明理由．

已知函数f（x），x∈R，对任意x₁、x₂∈R，均有f（x₁+x₂）=f（x₁）+f（x₂），又x＞0时，f（x）＜0，f（1）=a，试判断函数f（x）在[-3，3]上是否有最值．

在平面直角坐标系中，已知椭圆C：

=1（a＞b＞0）的左右顶点为A、B，直线l₁、l₂分别过点A、B且与x轴垂直，点（1，e）和（2，0）均在椭圆上，其中e为椭圆C的离心率．
（1）求椭圆C的方程；
（2）已知点P是椭圆C上不同于点A、B的任意一点，直线AP与l₂交于点D，直线BP与l₁于点E，线段OD和OE分别与椭圆交于点R，G．
（ⅰ）是否存在定圆与直线DE相切？若存在，求出该定圆的方程；若不存在，请说明理由；
（ⅱ）求证：

OG2

OR2

为定值．

某公司将6个招聘名额分给3个下属单位，一个单位3个名额，一个单位2个名额，一个单位1个名额，一共有

种不同的分配方案．

试题分类