Question

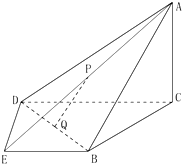如图，在四棱锥A-BCDE中，平面ABC⊥平面BCDE，∠CDE=∠BED=90°，AB=CD=2，DE=BE=1，AC=

2

．
（1）证明：DE⊥平面ACD；
（2）（文科）点P、Q分别为AE、BD的中点．求证：PQ∥平面ADC．
（3）（理科）求二面角B-AD-E的大小．

Answer 1

考点：二面角的平面角及求法,直线与平面平行的判定,直线与平面垂直的判定

专题：空间位置关系与距离,空间角

分析：（1）AC⊥DE，又DE⊥DC，从而DE⊥平面ACD；（2）PQ∥AO，而PQ?平面ADC，所以PQ∥平面ADC；（3）利用向量法求解．

解答： 解：（1）在直角梯形BCDE中，由DE=BE=1，CD=2得，BD=BC=

2

，由AC=

2

，AB=2，则AB²=AC²+BC²，即AC⊥BC，又平面ABC⊥平面BCDE，从而AC⊥平面BCDE，所以AC⊥DE，又DE⊥DC，从而DE⊥平面ACD；

（2）（文科）：取DC中点O，连接EO、AO，BO．则四边形DOBE为正方形，所以EO过点Q且Q平分EO，所以PQ∥AO，而PQ?平面ADC，所以PQ∥平面ADC．
（3）（理科）方法一：作BF⊥AD，与AD交于点F，过点F作FG∥DE，与AE交于点G，连结BG，由（ I）知，DE⊥AD，则FG⊥AD，所以∠BFG是二面角B-AD-E的平面角，在直角梯形BCDE中，由

CD²=BD²+BC²，得BD⊥BC，又平面ABC⊥平面BCDE，得BD⊥⊥平面ABC，从而，BD⊥AB，由于AC⊥平面BCDE，得：AC⊥CD，在Rt△ACD中，由CD=2，AC=

2

，得AD=

6

，
在Rt△AED中，DE=1，AD=

6

，得AE=

7

，在Rt△ABD中，BD=

2

，AB=2，AD=

6

，得BF=

2 3

3

，AF=

2

3

AD，从而GF=

2

3

，在△ABE，△ABG中，利用余弦定理分别可得cos∠BAE=

5 7

14

，BG=

2

3

，在△BFG中，cos∠BFG=

GF2+BF2-BG2

2BF•GF

=

3

2

，所以∠BFG=

π

6

，即二面角B-AD-E的大小是

π

6

．
方法二：以D为原点，分别以射线DE，DC为x，y轴的正半轴，建立空间直角坐标系D-xyz如图所示，由题意可知各点坐标如下：

D（0，0，0），E（1，0，0），C（0，2，0），A（0，2，

2

），B（1，1，0），设平面ADE的法向量为

m

=（x₁，y₁，z₁），平面ABD的法向量为

n

=（x₂，y₂，z₂），可算得

AD

=（0，-2，-

2

），

DB

=（1，1，0），

AE

=（1，-2，-

2

），由

m • AD =0 m • AE =0

得，

0-2y1- 2 z1=0 x1-2y1- 2 z1=0

，可取

m

=（0，1，-

2

），由

n • AD =0 n • BD =0

得，

0-2y2- 2 z2=0 x2+y2=0

，可取

n

=（1，-1，

2

），于是cos＜

m

，

n

＞=

m • n

| m || n |

=

3

2

，由题意可知，所求二面角是锐角，故二面角B-AD-E的大小是

π

6

．

点评：本题主要考查空间点、线、面位置关系，二面角等基础知识，同时考查空间想象能力，推理论证能力和运算求解能力．