题目内容
已知等差数列{an}的前n项和为Sn,且满足Sn=n2-n.
(Ⅰ)求an;
(Ⅱ)设数列{bn}满足bn+1=2bn-an且b1=4,
(i)证明:数列{bn-2n}是等比数列,并求{bn}的通项;
(ii)当n≥2时,比较bn-1•bn+1与bn2的大小.
(Ⅰ)求an;
(Ⅱ)设数列{bn}满足bn+1=2bn-an且b1=4,
(i)证明:数列{bn-2n}是等比数列,并求{bn}的通项;
(ii)当n≥2时,比较bn-1•bn+1与bn2的大小.
考点:数列递推式
专题:等差数列与等比数列
分析:(Ⅰ)由an=
,利用已知条件能求出an=2n-2.
(Ⅱ)(i)由已知得bn+1-2(n+1)=2(bn-2n),且b1-2=2,由此能证明数列{bn-2n}是以2为首项,2为公比的等比数列,从而得到bn=2n+2n.
(ii)当n≥2时,利用作差法得到bn-1•bn+1-bn2=2n(n-3)-4,由此能比较bn-1•bn+1与bn2的大小.
|
(Ⅱ)(i)由已知得bn+1-2(n+1)=2(bn-2n),且b1-2=2,由此能证明数列{bn-2n}是以2为首项,2为公比的等比数列,从而得到bn=2n+2n.
(ii)当n≥2时,利用作差法得到bn-1•bn+1-bn2=2n(n-3)-4,由此能比较bn-1•bn+1与bn2的大小.
解答:
(Ⅰ)解:∵Sn=n2-n,
∴当n=1时,a1=S1=0,
当n≥2时,an=Sn-Sn-1=n2-n-[(n-1)2-(n-1)]=2n-2,
∵n=1时满足上式,
∴an=2n-2.
(Ⅱ)(i)证明:由已知得bn+1=2bn-2n+2,
即bn+1-2(n+1)=2(bn-2n),且b1-2=2,
∴数列{bn-2n}是以2为首项,2为公比的等比数列,
则bn-2n=2n,∴bn=2n+2n.
(ii)解:当n≥2时,∵bn-1•bn+1-bn2
=[2n-1+2(n-1)]•[2n+1+2(n+1)]-(2n+2n)2
=22n+2n(n+1)+2n×4(n-1)+4(n2-1)-(22n+4n×2n+4n2)
=2n(n-3)-4,
∴当n=2或n=3时,bn-1•bn+1<bn2,
当n≥4时,bn-1•bn+1>bn2.
∴当n=1时,a1=S1=0,
当n≥2时,an=Sn-Sn-1=n2-n-[(n-1)2-(n-1)]=2n-2,
∵n=1时满足上式,
∴an=2n-2.
(Ⅱ)(i)证明:由已知得bn+1=2bn-2n+2,
即bn+1-2(n+1)=2(bn-2n),且b1-2=2,
∴数列{bn-2n}是以2为首项,2为公比的等比数列,
则bn-2n=2n,∴bn=2n+2n.
(ii)解:当n≥2时,∵bn-1•bn+1-bn2
=[2n-1+2(n-1)]•[2n+1+2(n+1)]-(2n+2n)2
=22n+2n(n+1)+2n×4(n-1)+4(n2-1)-(22n+4n×2n+4n2)
=2n(n-3)-4,
∴当n=2或n=3时,bn-1•bn+1<bn2,
当n≥4时,bn-1•bn+1>bn2.
点评:本题考查数列的通项公式的求法,考查等比数列的证明,考查两个式子大小的比较,解题时要认真审题,注意构造法的合理运用.

练习册系列答案
相关题目
若a1=12,a2=12+22+12,…,an=12+22+…+n2+…+22+12,在运用数学归纳法证明an=
n(2n2+1)时,第二步中从k到k+1应添加的项是( )
| 1 |
| 3 |
| A、k2+1 |
| B、(k2+1)2 |
| C、(k+1)2+k2 |
| D、(k+1)2+2k2 |
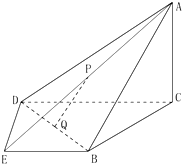 如图,在四棱锥A-BCDE中,平面ABC⊥平面BCDE,∠CDE=∠BED=90°,AB=CD=2,DE=BE=1,AC=
如图,在四棱锥A-BCDE中,平面ABC⊥平面BCDE,∠CDE=∠BED=90°,AB=CD=2,DE=BE=1,AC=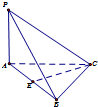 如图,在三棱锥P-ABC中,已知AB=2,AC=AP=4,PB=2
如图,在三棱锥P-ABC中,已知AB=2,AC=AP=4,PB=2