题目内容
已知函数f(x)=
(0<θ<π),且f(x)≤x对?x>0恒成立.数列{an}满足a1=f(1),an+1=
an+
(n∈N*).
(1)求θ的取值集合;
(2)设bn=an-
,求数列{bn}的通项公式;
(3)数列{cn}中,c1=1,cn+1=(1+an)cn,求证:cn<e2.(e为自然对数的底数)
| lnx+1 |
| sinθ |
| 1 |
| 2 |
| n2-2n-1 |
| 4n2(n+1)2 |
(1)求θ的取值集合;
(2)设bn=an-
| 1 |
| 2n2 |
(3)数列{cn}中,c1=1,cn+1=(1+an)cn,求证:cn<e2.(e为自然对数的底数)
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(1)f(x)≤x对?x>0恒成立等价于sinθ≥
对?x>0恒成立.设g(x)=
(x>0),则sinθ≥g(x)max.由此能求出θ的取值集合.
(2)f(x)=lnx+1,a1=f(1)=1.由bn=an-
,推导出数列{bn}是首项为b1=a1-
=
,公比为
的等比数列.由此能求出bn=
(n∈N*).
(3)由bn=an-
=
,得an=
+
.则cn+1=(1+
+
)cn,两边取自然对数,得lncn+1=ln(1+
+
)+lncn,由lnx≤x-1对?x>0恒成立,能证明cn<e2.
| lnx+1 |
| x |
| lnx+1 |
| x |
(2)f(x)=lnx+1,a1=f(1)=1.由bn=an-
| 1 |
| 2n2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2n |
(3)由bn=an-
| 1 |
| 2n2 |
| 1 |
| 2n |
| 1 |
| 2n |
| 1 |
| 2n2 |
| 1 |
| 2n |
| 1 |
| 2n2 |
| 1 |
| 2n |
| 1 |
| 2n2 |
解答:
(1)解:由0<θ<π得sinθ>0,
故f(x)≤x对?x>0恒成立等价于sinθ≥
对?x>0恒成立.
设g(x)=
(x>0),则sinθ≥g(x)max.
由于g′(x)=
,令g'(x)=0,得x=1.
∵当x∈(0,1)时,g'(x)>0,g(x)递增;
当x∈(1,+∞)时,g'(x)<0,g(x)递减.
∴g(x)max=g(1)=1,∴sinθ≥1.
又0<sinθ≤1,∴sinθ=1,θ=
.
∴θ的取值集合为{
}.
(2)解:由(1)知,f(x)=lnx+1,a1=f(1)=1.
∵bn=an-
,
∴bn+1=an+1-
=
an+
-
=
an-
=
(an-
)=
bn.
∴数列{bn}是首项为b1=a1-
=
,公比为
的等比数列.
∴bn=
(n∈N*).
(3)证明:由(2)知,bn=an-
=
,得an=
+
.
则cn+1=(1+
+
)cn,又c1=1知cn>0,
两边取自然对数,得lncn+1=ln(1+
+
)+lncn,
由(1)知,f(x)=lnx+1≤x,即lnx≤x-1对?x>0恒成立,
∴lncn+1-lncn=ln(1+
+
)≤
+
=
+
<
+
=
+(
-
),
∴lnc2-lnc1<
+(1-
),lnc3-lnc2<
+(
-
),
…lncn-lncn-1<
+(
-
)(n≥2).
把以上n-1个是式子相加,注意到lnc1=ln1=0,得lncn<
+
+…+
+(1-
)=2-
-
<2(n≥2).
当n=1时,lnc1=0<2也满足上式,
∴cn<e2.
故f(x)≤x对?x>0恒成立等价于sinθ≥
| lnx+1 |
| x |
设g(x)=
| lnx+1 |
| x |
由于g′(x)=
| -lnx |
| x2 |
∵当x∈(0,1)时,g'(x)>0,g(x)递增;
当x∈(1,+∞)时,g'(x)<0,g(x)递减.
∴g(x)max=g(1)=1,∴sinθ≥1.
又0<sinθ≤1,∴sinθ=1,θ=
| π |
| 2 |
∴θ的取值集合为{
| π |
| 2 |
(2)解:由(1)知,f(x)=lnx+1,a1=f(1)=1.
∵bn=an-
| 1 |
| 2n2 |
∴bn+1=an+1-
| 1 |
| 2(n+1)2 |
| 1 |
| 2 |
| n2-2n-1 |
| 4n2(n+1)2 |
| 1 |
| 2(n+1)2 |
| 1 |
| 2 |
| 1 |
| 4n2 |
| 1 |
| 2 |
| 1 |
| 2n2 |
| 1 |
| 2 |
∴数列{bn}是首项为b1=a1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴bn=
| 1 |
| 2n |
(3)证明:由(2)知,bn=an-
| 1 |
| 2n2 |
| 1 |
| 2n |
| 1 |
| 2n |
| 1 |
| 2n2 |
则cn+1=(1+
| 1 |
| 2n |
| 1 |
| 2n2 |
两边取自然对数,得lncn+1=ln(1+
| 1 |
| 2n |
| 1 |
| 2n2 |
由(1)知,f(x)=lnx+1≤x,即lnx≤x-1对?x>0恒成立,
∴lncn+1-lncn=ln(1+
| 1 |
| 2n |
| 1 |
| 2n2 |
| 1 |
| 2n |
| 1 |
| 2n2 |
| 1 |
| 2n |
| 2 |
| 4n2 |
<
| 1 |
| 2n |
| 2 |
| 4n2-1 |
| 1 |
| 2n |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
∴lnc2-lnc1<
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 22 |
| 1 |
| 3 |
| 1 |
| 5 |
…lncn-lncn-1<
| 1 |
| 2n-1 |
| 1 |
| 2n-3 |
| 1 |
| 2n-1 |
把以上n-1个是式子相加,注意到lnc1=ln1=0,得lncn<
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 2n-1 |
| 1 |
| 2n-1 |
| 1 |
| 2n-1 |
| 1 |
| 2n-1 |
当n=1时,lnc1=0<2也满足上式,
∴cn<e2.
点评:本题考查数列的通项公式的求法,考查不等式的证明,解题时要认真审题,注意对数性质、导数性质的合理运用.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案
相关题目
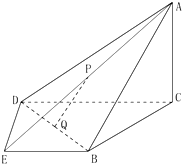 如图,在四棱锥A-BCDE中,平面ABC⊥平面BCDE,∠CDE=∠BED=90°,AB=CD=2,DE=BE=1,AC=
如图,在四棱锥A-BCDE中,平面ABC⊥平面BCDE,∠CDE=∠BED=90°,AB=CD=2,DE=BE=1,AC=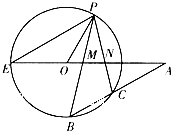 如图,E,P,B,C为圆O上的四点,直线PB,PC,BC分别交直线EO于M,N三点,且PM=PN.
如图,E,P,B,C为圆O上的四点,直线PB,PC,BC分别交直线EO于M,N三点,且PM=PN.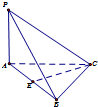 如图,在三棱锥P-ABC中,已知AB=2,AC=AP=4,PB=2
如图,在三棱锥P-ABC中,已知AB=2,AC=AP=4,PB=2