题目内容
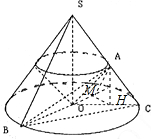
 如图,已知底面圆半径为4的圆锥SO中,S为顶点,O为底面圆心,SB、SC是母线,∠BOC=120°,作OA⊥SC于A点,若将△SAO绕轴旋转一周所得几何体的体积是圆锥SO体积的
如图,已知底面圆半径为4的圆锥SO中,S为顶点,O为底面圆心,SB、SC是母线,∠BOC=120°,作OA⊥SC于A点,若将△SAO绕轴旋转一周所得几何体的体积是圆锥SO体积的| 1 |
| 4 |
(Ⅰ)求圆锥SO的体积;
(Ⅱ)在△SAO绕轴SO旋转一周过程中(此时C点不动),求二面角A-OB-C余弦值的取值范围.
考点:与二面角有关的立体几何综合题,旋转体(圆柱、圆锥、圆台)
专题:
分析:(Ⅰ)先求出由A点旋转形成的截面圆的半径,可得A为SC的中点,从而可求圆锥SO的体积;
(Ⅱ)分类讨论,当A∈平面SOB时,二面角A-OB-C余弦值为0;当A∉平面SOB时,作出二面角A-OB-C的平面角,再求二面角A-OB-C余弦值的取值范围.
(Ⅱ)分类讨论,当A∈平面SOB时,二面角A-OB-C余弦值为0;当A∉平面SOB时,作出二面角A-OB-C的平面角,再求二面角A-OB-C余弦值的取值范围.
解答:
 解:(Ⅰ)记由A点旋转形成的截面圆为圆O1,则
解:(Ⅰ)记由A点旋转形成的截面圆为圆O1,则
∵将△SAO绕轴旋转一周所得几何体的体积是圆锥SO体积的
,
∴
=
,
∵OC=4,
∴O1A=2,即A为SC的中点,
∴圆锥SO的体积
•π•43=
π;
(Ⅱ)在△SAO绕轴SO旋转一周过程中,当A∈平面SOB时,平面ABO⊥平面BOC,此时二面角A-OB-C余弦值为0;
当A∉平面SOB时,作AH∥SO,∴AH⊥圆O,作HM⊥BO交BO延长线于M,连接AM,则AH⊥OM,
∵HM∩AH=H,∴BO⊥平面AHM,∴BO⊥AM,
记二面角A-OB-C的大小为θ,则θ=∠AMH或π-∠AMH.
在Rt△AHM中,AH=
SO=2,H到线段BO的距离d∈(0,2],
∴|cosθ|=cos∠AMH=
=
∈(0,
],
综上所述,二面角A-OB-C余弦值的取值范围为[-
,
].
 解:(Ⅰ)记由A点旋转形成的截面圆为圆O1,则
解:(Ⅰ)记由A点旋转形成的截面圆为圆O1,则∵将△SAO绕轴旋转一周所得几何体的体积是圆锥SO体积的
| 1 |
| 4 |
∴
| O1A2 |
| OC2 |
| 1 |
| 4 |
∵OC=4,
∴O1A=2,即A为SC的中点,
∴圆锥SO的体积
| 1 |
| 3 |
| 64 |
| 3 |
(Ⅱ)在△SAO绕轴SO旋转一周过程中,当A∈平面SOB时,平面ABO⊥平面BOC,此时二面角A-OB-C余弦值为0;
当A∉平面SOB时,作AH∥SO,∴AH⊥圆O,作HM⊥BO交BO延长线于M,连接AM,则AH⊥OM,
∵HM∩AH=H,∴BO⊥平面AHM,∴BO⊥AM,
记二面角A-OB-C的大小为θ,则θ=∠AMH或π-∠AMH.
在Rt△AHM中,AH=
| 1 |
| 2 |
∴|cosθ|=cos∠AMH=
| d | ||
|
|
| ||
| 2 |
综上所述,二面角A-OB-C余弦值的取值范围为[-
| ||
| 2 |
| ||
| 2 |
点评:本题考查圆锥的体积,考查二面角A-OB-C余弦值的取值范围,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
过△ABC所在平面α外一点P,作PO⊥α,垂足为O,连接PA,PB,PC.若PA=PB=PC,则点O是△ABC的( )
| A、垂心 | B、外心 | C、内心 | D、重心 |
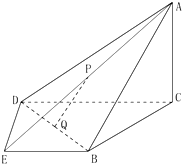 如图,在四棱锥A-BCDE中,平面ABC⊥平面BCDE,∠CDE=∠BED=90°,AB=CD=2,DE=BE=1,AC=
如图,在四棱锥A-BCDE中,平面ABC⊥平面BCDE,∠CDE=∠BED=90°,AB=CD=2,DE=BE=1,AC= 如图,已知几何体的底面ABCD为正方形,AC∩DB=N,PD⊥面ABCD,EC∥PD,PD=CD=2EC=2.
如图,已知几何体的底面ABCD为正方形,AC∩DB=N,PD⊥面ABCD,EC∥PD,PD=CD=2EC=2.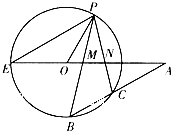 如图,E,P,B,C为圆O上的四点,直线PB,PC,BC分别交直线EO于M,N三点,且PM=PN.
如图,E,P,B,C为圆O上的四点,直线PB,PC,BC分别交直线EO于M,N三点,且PM=PN.