题目内容
 如图,已知椭圆C:
如图,已知椭圆C:| y2 |
| a2 |
| x2 |
| b2 |
| 1 |
| 2 |
(1)求椭圆C的标准方程;
(2)求
| QM |
| QN |
(3)设点P是椭圆C上异于M,N的任意一点,且直线MP,NP分别与y轴交于点R,S,O为坐标原点,求证:OR•OS为定值.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由已知得
,由此能求出椭圆C的标准方程.
(2)由题意设M(x1,y1),N(-x1,y1),Q(0,2),
=(x1,y1-2),
=(-x1,y1-2),由此能求出y1=
时,
•
的最小值是
,圆Q的方程为:x2+(y-2)2=
.
(3)设P(x0,y0),MP:y-y0=
(x-x0),求出R(0,
),同理,S(0,
),由此能证明OR•OS=|
|=4为定值.
|
(2)由题意设M(x1,y1),N(-x1,y1),Q(0,2),
| QM |
| QN |
| 8 |
| 7 |
| QM |
| QN |
| 9 |
| 7 |
| 135 |
| 49 |
(3)设P(x0,y0),MP:y-y0=
| y0-y1 |
| x0-x1 |
| y0x1-x0y1 |
| x0-x1 |
| -y0x1-x0y1 |
| x0+x1 |
| x02y12-x12y02 |
| x02-x12 |
解答:
(1)解:∵椭圆C:
+
=1(a>b>0)的离心率为
,
以椭圆C的上顶点Q为圆心作圆Q:x2+(y-2)2=r2(r>0),
∴
,解得a=2,b=
,
∴椭圆C的标准方程为
+
=1.
(2)解:由题意设M(x1,y1),N(-x1,y1),Q(0,2),
=(x1,y1-2),
=(-x1,y1-2),
∴
•
=-x12+(y1-2)2=
y12-4y1+1=
(y1-
)2-
,
∴y1=
时,
•
的最小值是
,
x1=±
,r2=
+
=
,
∴圆Q的方程为:x2+(y-2)2=
.
(3)证明:设P(x0,y0),MP:y-y0=
(x-x0),
令x=0,y=
,R(0,
),
同理,S(0,
),
∴OR•OS=|
|,
又
+
=1,
+
=1,
∴OR•OS=|
|=4为定值.
| y2 |
| a2 |
| x2 |
| b2 |
| 1 |
| 2 |
以椭圆C的上顶点Q为圆心作圆Q:x2+(y-2)2=r2(r>0),
∴
|
| 3 |
∴椭圆C的标准方程为
| x2 |
| 3 |
| y2 |
| 4 |
(2)解:由题意设M(x1,y1),N(-x1,y1),Q(0,2),
| QM |
| QN |
∴
| QM |
| QN |
| 7 |
| 4 |
| 7 |
| 4 |
| 8 |
| 7 |
| 9 |
| 7 |
∴y1=
| 8 |
| 7 |
| QM |
| QN |
| 9 |
| 7 |
x1=±
3
| ||
| 7 |
| 99 |
| 49 |
| 36 |
| 49 |
| 135 |
| 49 |
∴圆Q的方程为:x2+(y-2)2=
| 135 |
| 49 |
(3)证明:设P(x0,y0),MP:y-y0=
| y0-y1 |
| x0-x1 |
令x=0,y=
| y0x1-x0y1 |
| x0-x1 |
| y0x1-x0y1 |
| x0-x1 |
同理,S(0,
| -y0x1-x0y1 |
| x0+x1 |
∴OR•OS=|
| x02y12-x12y02 |
| x02-x12 |
又
| y02 |
| 4 |
| x02 |
| 3 |
| y12 |
| 4 |
| x12 |
| 3 |
∴OR•OS=|
| x02y12-x12y02 |
| x02-x12 |
点评:本题考查椭圆C的标准方程的求法,考查
•
的最小值和此时圆Q的方程的求法,考查OR•OS为定值的证明,解题时要注意函数与方程思想的合理运用.
| QM |
| QN |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
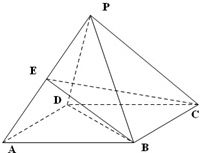 已知四棱锥P-ABCD的底面是正方形,PB=PD,E为PA的中点.
已知四棱锥P-ABCD的底面是正方形,PB=PD,E为PA的中点.