题目内容
已知向量
=(2
sin
,2),
=(cos
,cos2
).函数f(x)=
•
.
(Ⅰ)若f(x)=
,求cos(x+
)的值;
(Ⅱ)在△ABC中,角A、B、C的对边分别是a、b、c,且满足(2a-c)cosB=bcosC,求f(A)的取值范围.
| m |
| 3 |
| x |
| 4 |
| n |
| x |
| 4 |
| x |
| 4 |
| m |
| n |
(Ⅰ)若f(x)=
| 1 |
| 2 |
| π |
| 3 |
(Ⅱ)在△ABC中,角A、B、C的对边分别是a、b、c,且满足(2a-c)cosB=bcosC,求f(A)的取值范围.
考点:正弦定理的应用,平面向量的综合题
专题:解三角形,平面向量及应用
分析:(I)利用数量积运算、倍角公式、两角和差的正弦公式可得函数f(x)=
•
=2sin(
+
)+1.
由于f(x)=
,可得sin(
+
)=-
.再利用倍角公式可得cos(x+
)=1-2sin2(
+
)..
(II)由(2a-c)cosB=bcosC,利用正弦定理可得:2sinAcosB-sinCcosB=sinBcosC,化为2sinAcosB=sin(B+C)=
sinA,再利用正弦函数的单调性即可得出.
| m |
| n |
| x |
| 2 |
| π |
| 6 |
由于f(x)=
| 1 |
| 2 |
| x |
| 2 |
| π |
| 6 |
| 1 |
| 4 |
| π |
| 3 |
| x |
| 2 |
| π |
| 6 |
(II)由(2a-c)cosB=bcosC,利用正弦定理可得:2sinAcosB-sinCcosB=sinBcosC,化为2sinAcosB=sin(B+C)=
sinA,再利用正弦函数的单调性即可得出.
解答:
解:(I)函数f(x)=
•
=2
sin
cos
+2cos2
=
sin
+cos
+1=2sin(
+
)+1.
∵f(x)=
,
∴2sin(
+
)+1=
,化为sin(
+
)=-
.
∴cos(x+
)=1-2sin2(
+
)=1-2×(-
)2=
.
(II)∵(2a-c)cosB=bcosC,
利用正弦定理可得:2sinAcosB-sinCcosB=sinBcosC,
化为2sinAcosB=sin(B+C)=sinA,
∵sinA≠0,∴cosB=
,∵B∈(0,π),
∴B=
.∴0<A<
,
<
+
<
,
∴
<sin(
+
)<1,
∴2<f(A)<3.
| m |
| n |
=2
| 3 |
| x |
| 4 |
| x |
| 4 |
| x |
| 4 |
=
| 3 |
| x |
| 2 |
| x |
| 2 |
| x |
| 2 |
| π |
| 6 |
∵f(x)=
| 1 |
| 2 |
∴2sin(
| x |
| 2 |
| π |
| 6 |
| 1 |
| 2 |
| x |
| 2 |
| π |
| 6 |
| 1 |
| 4 |
∴cos(x+
| π |
| 3 |
| x |
| 2 |
| π |
| 6 |
| 1 |
| 4 |
| 7 |
| 8 |
(II)∵(2a-c)cosB=bcosC,
利用正弦定理可得:2sinAcosB-sinCcosB=sinBcosC,
化为2sinAcosB=sin(B+C)=sinA,
∵sinA≠0,∴cosB=
| 1 |
| 2 |
∴B=
| π |
| 3 |
| 2π |
| 3 |
| π |
| 6 |
| A |
| 2 |
| π |
| 6 |
| π |
| 2 |
∴
| 1 |
| 2 |
| A |
| 2 |
| π |
| 6 |
∴2<f(A)<3.
点评:本题主要考查了数量积运算、正弦定理、两角和差的正弦函数、正弦函数的单调性、诱导公式等基础知识与基本技能方法,考查了计算能力与推理能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
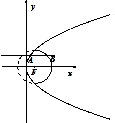 如图所示,直线y=m与抛物线y2=8x交与点A,与圆(x-2)2+y2=16的实线部分交于点B,F为抛物线的焦点,则△ABF的周长的取值范围是( )
如图所示,直线y=m与抛物线y2=8x交与点A,与圆(x-2)2+y2=16的实线部分交于点B,F为抛物线的焦点,则△ABF的周长的取值范围是( )| A、(6,8) |
| B、(4,6) |
| C、(8,12) |
| D、(8,10) |