题目内容
已知点M(3,1),直线ax-y+4=0及圆(x-1)2+(y-2)2=4
(1)求过M点的圆的切线方程
(2)若直线ax-y+4=0与圆相交于A,B两点,且弦AB的长为2
,求a的值
(3)若电P(x,y)是圆上的任意一点,求k=
的取值范围.
(1)求过M点的圆的切线方程
(2)若直线ax-y+4=0与圆相交于A,B两点,且弦AB的长为2
| 3 |
(3)若电P(x,y)是圆上的任意一点,求k=
| y-4 |
| x |
考点:直线和圆的方程的应用
专题:计算题,作图题,直线与圆
分析:(1)设过M点的圆的切线方程为x=m(y-1)+3,与圆的方程联立消元再令判别式为0即可;
(2)直线ax-y+4=0与圆相交于A,B两点,且弦AB的长为2
可化为圆心到直线ax-y+4=0的距离为
=1;从而求解.
(3)k=
的几何意义是点P(x,y),与点(0,4)连线的直线的斜率,故设过点(0,4)的直线方程可设为kx-y+4=0;联立解△≥0即可.
(2)直线ax-y+4=0与圆相交于A,B两点,且弦AB的长为2
| 3 |
| 4-3 |
(3)k=
| y-4 |
| x |
解答:
 解:(1)设过M点的圆的切线方程为x=m(y-1)+3;
解:(1)设过M点的圆的切线方程为x=m(y-1)+3;
与(x-1)2+(y-2)2=4联立消x得,
(m2+1)y2-2(m2-2m+2)y+(m-2)2=0;
故△=4(m2-2m+2)2-4(m2+1)(m-2)2=0,
化简得,3m2-4m=0;
故m=0或m=
;
故过M点的圆的切线方程为x-3=0或3x-4y-5=0;
(2)∵直线ax-y+4=0与圆相交于A,B两点,且弦AB的长为2
,
∴圆心到直线ax-y+4=0的距离为
=1;
即d=
=1,
解得,a=-
;
(3)k=
的几何意义是点P(x,y),与点(0,4)连线的直线的斜率,
过点(0,4)的直线方程可设为kx-y+4=0;
与(x-1)2+(y-2)2=4联立消y得,
(k2+1)x2+(4k-2)x+1=0,
故△=(4k-2)2-4(k2+1)≥0,
解得,k≤0或k≥
.
 解:(1)设过M点的圆的切线方程为x=m(y-1)+3;
解:(1)设过M点的圆的切线方程为x=m(y-1)+3;与(x-1)2+(y-2)2=4联立消x得,
(m2+1)y2-2(m2-2m+2)y+(m-2)2=0;
故△=4(m2-2m+2)2-4(m2+1)(m-2)2=0,
化简得,3m2-4m=0;
故m=0或m=
| 4 |
| 3 |
故过M点的圆的切线方程为x-3=0或3x-4y-5=0;
(2)∵直线ax-y+4=0与圆相交于A,B两点,且弦AB的长为2
| 3 |
∴圆心到直线ax-y+4=0的距离为
| 4-3 |
即d=
| |a-2+4| | ||
|
解得,a=-
| 3 |
| 4 |
(3)k=
| y-4 |
| x |
过点(0,4)的直线方程可设为kx-y+4=0;
与(x-1)2+(y-2)2=4联立消y得,
(k2+1)x2+(4k-2)x+1=0,
故△=(4k-2)2-4(k2+1)≥0,
解得,k≤0或k≥
| 4 |
| 3 |
点评:本题全面都考查了直线与圆的位置关系的应用,同时考查了学生的作图能力,属于中档题.

练习册系列答案
相关题目
某棱柱如图所示放置,则该棱柱的正视图是( )


A、 |
B、 |
C、 |
D、 |
若
、
、
是空间不共面的三个向量,则与向量
+
和向量
-
构成不共面的向量是( )
| OA |
| OB |
| OC |
| OA |
| OB |
| OA |
| OB |
A、
| ||
B、
| ||
C、
| ||
D、
|
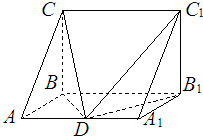 如图,在直三棱柱ABC-A1B1C1中,AB⊥BC,BC=
如图,在直三棱柱ABC-A1B1C1中,AB⊥BC,BC=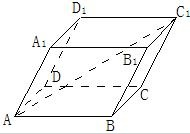 如图,在平行六面体ABCD-A1B1C1D1中,AB=AD=AA1=1,∠BAD=60°,∠BAA1=∠DAA1=45°.
如图,在平行六面体ABCD-A1B1C1D1中,AB=AD=AA1=1,∠BAD=60°,∠BAA1=∠DAA1=45°.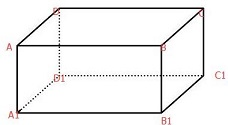 如图,在长方体ABCD-A1B1C1D1中,AB=6,AD=3
如图,在长方体ABCD-A1B1C1D1中,AB=6,AD=3