题目内容
3.若函数f(x)=lnx-ax+1,a∈R有两个零点,则实数a的取值范围是( )| A. | (-∞,1) | B. | (0,1) | C. | (-1,1) | D. | (1,2) |
分析 由题意可得f(x)=0即a=$\frac{lnx+1}{x}$有两个不等的实数解.令g(x)=$\frac{lnx+1}{x}$,求出导数和单调区间、极值和最值,画出图象,通过图象即可得到结论.
解答 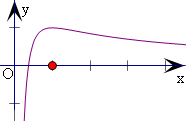 解:函数f(x)=lnx-ax+1,a∈R有两个零点,
解:函数f(x)=lnx-ax+1,a∈R有两个零点,
等价为f(x)=0即a=$\frac{lnx+1}{x}$有两个不等的实数解.
令g(x)=$\frac{lnx+1}{x}$,g′(x)=$\frac{-lnx}{{x}^{2}}$,
当x>1时,g′(x)<0,g(x)递减;当0<x<1时,g′(x)>0,g(x)递增.
g(x)在x=1处取得极大值,且为最大值1.
当x→+∞,y→0.
画出函数y=g(x)的图象,
由图象可得0<a<1时,y=g(x)和y=a有两个交点,
即方程有两个不等实数解,f(x)有两个零点.
故选:B.
点评 本题考查函数的零点问题,注意运用转化思想,考查构造函数法,运用导数判断单调性,考查数形结合的思想方法,属于中档题.

练习册系列答案
相关题目
1.在△ABC中,A、B、C所对的边分别是a、b、c,已知a2+b2=c2+$\sqrt{3}$ab,则C=( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{3}$或$\frac{2π}{3}$ | D. | $\frac{π}{6}$或$\frac{5π}{6}$ |
2.已知0<c<1,a>b>1,下列不等式成立的是( )
| A. | ca>cb | B. | $\frac{a}{a-c}>\frac{b}{b-c}$ | C. | bac>abc | D. | logac>logbc |
19.(文)已知x,y满足(1+i)+(2-3i)=a+bi,则a,b分别等于( )
| A. | 3,-2 | B. | 3,2 | C. | 3,-3 | D. | -1,4 |
6.在△ABC中,若B=2A,$a:b=1:\sqrt{3}$,则A=( )
| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
15.已知等差数列{an}满足a3+a13-a8=2,则{an}的前15项和S15=( )
| A. | 60 | B. | 30 | C. | 15 | D. | 10 |
12.已知复数z=(a-4)+(a+2)i(a∈R),则“a=2”是“z为纯虚数”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 既不充分也不必要条件 | D. | 充要条件 |
13.在等比数列{an}中,已知${a_1}+{a_2}=-\frac{3}{2},{a_4}+{a_5}=12$,则数列是( )
| A. | 递增数列 | B. | 递减数列 | C. | 摆动数列 | D. | 常数列 |