题目内容
19.已知sinα+cosα=$\frac{1}{5}$,则sinα•cosα的值为( )| A. | $\frac{12}{25}$ | B. | -$\frac{12}{25}$ | C. | -$\frac{7}{5}$ | D. | $\frac{7}{5}$ |
分析 根据同角三角函数关系式化简即可求值.
解答 解:由sinα+cosα=$\frac{1}{5}$,
可得(sinα+cosα)2=$\frac{1}{25}$,
即1+2sinαcosα=$\frac{1}{25}$,
∴sinα•cosα=$-\frac{12}{25}$.
故选B.
点评 本题主要考察了同角三角函数关系式的应用,属于基本知识的考查.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.已知△ABC,AB=4,BC=3,AC=5,现以AB为轴旋转一周,则所得几何体的表面积( )
| A. | 24π | B. | 21 π | C. | 33π | D. | 39 π |
14.若角α∈(-π,-$\frac{π}{2}$),则$\sqrt{\frac{1+cosα}{1-cosα}}$-$\sqrt{\frac{1-cosα}{1+cosα}}$=( )
| A. | -2tanα | B. | 2tanα | C. | $\frac{-2}{tanα}$ | D. | $\frac{2}{tanα}$ |
11.如图,该算法输出的结果是( )


| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{5}$ |
8.设F1,F2分别是椭圆$E:{x^2}+\frac{y^2}{b^2}=1(0<b<1)$的左、右焦点,已知点F1的直线交椭圆E于A,B两点,若|AF1|=2|BF1|,AF2⊥x轴,则椭圆E的方程为( )
| A. | ${x^2}+\frac{{3{y^2}}}{2}=1$ | B. | ${x^2}+\frac{{6{y^2}}}{5}=1$ | C. | ${x^2}+\frac{{5{y^2}}}{4}=1$ | D. | ${x^2}+\frac{{8{y^2}}}{7}=1$ |
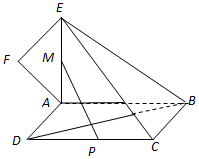 如图,正方形ABCD所在平面与四边形ABEF所在平面互相垂直,△ABE是等腰直角三角形,AB=AE,FA=FE,∠AEF=45°.
如图,正方形ABCD所在平面与四边形ABEF所在平面互相垂直,△ABE是等腰直角三角形,AB=AE,FA=FE,∠AEF=45°.