题目内容
15.若奇函数f(x)是定义在(-1,1)上的奇函数,且在[0,1)上递增,解关于a的不等式:f(a-2)+f(a2-4)<0.分析 根据函数奇偶性和单调性的关系将不等式转化不等式组进行求解即可.
解答 解:∵奇函数f(x)是定义在(-1,1)上的奇函数,且在[0,1)上递增,
∴奇函数f(x)是定义在(-1,1)上的为增函数,
则f(a-2)+f(a2-4)<0.等价为f(a2-4)<-f(a-2)=f(2-a).
即$\left\{\begin{array}{l}{-1<a-2<1}\\{-1<{a}^{2}-4<1}\\{{a}^{2}-4<2-a}\end{array}\right.$,即$\left\{\begin{array}{l}{1<a<3}\\{3<{a}^{2}<5}\\{{a}^{2}+a-6<0}\end{array}\right.$,
即$\left\{\begin{array}{l}{1<a<3}\\{\sqrt{3}<a<\sqrt{5}或-\sqrt{5}<a<-\sqrt{3}}\\{-3<a<2}\end{array}\right.$,即$\sqrt{3}$<a<2,
即不等式的解集为($\sqrt{3}$,2).
点评 本题主要考查不等式的求解,根据函数奇偶性和单调性的关系将不等式进行转化是解决本题的关键.

练习册系列答案
 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
6.方程lgx+x=0的根所在的区间是( )
| A. | $(0,\frac{1}{4})$ | B. | $(\frac{1}{4},\frac{1}{2})$ | C. | $(\frac{1}{2},\frac{3}{4})$ | D. | $(\frac{3}{4},1)$ |
10.在等差数列{an}中,已知a6+a9+a13+a16=20,则S21等于( )
| A. | 100 | B. | 105 | C. | 200 | D. | 0 |
7.y=cos($\frac{x}{2}$-$\frac{π}{6}$)(-π≤x≤π)的值域为( )
| A. | [-$\frac{1}{2}$,$\frac{1}{2}$] | B. | [-1,1] | C. | [-$\frac{1}{2}$,1] | D. | [-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$] |
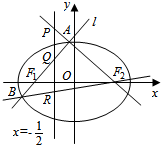 设F1,F2分别是椭圆C:$\frac{{x}^{2}}{2}$+y2=1的左、右焦点,过F1且斜率不为零的动直线l与椭圆C交于A,B两点.
设F1,F2分别是椭圆C:$\frac{{x}^{2}}{2}$+y2=1的左、右焦点,过F1且斜率不为零的动直线l与椭圆C交于A,B两点.