题目内容
20.过双曲线${x^2}-\frac{y^2}{3}=1$的右焦点作直线l交双曲线于A,B两点,则满足|AB|=6的直线l有( )条.| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
分析 双曲线的两个顶点之间的距离是2,小于4,过抛物线的焦点一定有两条直线使得交点之间的距离等于6,当直线与实轴垂直时,做出直线与双曲线交点的纵标,得到也是一条长度等于6的线段.
解答 解:∵双曲线的两个顶点之间的距离是2,小于4,
∴当直线与双曲线左右两支各有一个交点时,过双曲线的焦点一定有两条直线使得两交点之间的距离等于6,
当直线与实轴垂直时,有4-$\frac{{y}^{2}}{3}$=1,解得y=±3,
∴此时直线AB的长度是6,即只与右支有交点的弦长为4的线仅有一条.
综上可知有三条直线满足|AB|=6,
故选C.
点评 本题考查直线与双曲线之间的关系问题,本题解题的关键是看清楚当直线的斜率不存在,即直线与实轴垂直时,要验证线段的长度.

练习册系列答案
相关题目
8.在△ABC中,A=30°,B=60°,C=90°,那么三边之比a:b:c等于( )
| A. | 1:2:3 | B. | 3:2:1 | C. | 1:$\sqrt{3}$:2 | D. | 2:$\sqrt{3}$:1 |
5.sinx=$\frac{1}{2}$,则sin($\frac{π}{2}$+x)•tan(π-x)的值为( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
12.已知F是抛物线y2=4x的焦点,点A,B在该抛物线上且位于x轴的两侧,OA⊥OB(其中O为坐标原点),则△AOB与△AOF面积之和的最小值是( )
| A. | 16 | B. | 8$\sqrt{3}$ | C. | 8$\sqrt{5}$ | D. | 18 |
9.过点M(0,0),且平行于向量$\overrightarrow{a}$=(1,2)的直线方程是( )
| A. | x-2y=0 | B. | x+2y=0 | C. | 2x+y=0 | D. | 2x-y=0 |
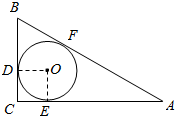 如图,在Rt△ABC中,∠C=90°,BC=a,AC=b,AB=c,⊙O为ABC的内切圆,D,E,F分别为切点,O的半径为r,试用含a,b,c的代数式表示r.
如图,在Rt△ABC中,∠C=90°,BC=a,AC=b,AB=c,⊙O为ABC的内切圆,D,E,F分别为切点,O的半径为r,试用含a,b,c的代数式表示r.