题目内容
5.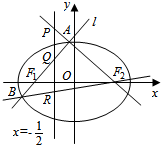 设F1,F2分别是椭圆C:$\frac{{x}^{2}}{2}$+y2=1的左、右焦点,过F1且斜率不为零的动直线l与椭圆C交于A,B两点.
设F1,F2分别是椭圆C:$\frac{{x}^{2}}{2}$+y2=1的左、右焦点,过F1且斜率不为零的动直线l与椭圆C交于A,B两点.(Ⅰ)求△AF1F2的周长;
(Ⅱ)若存在直线l,使得直线F2A,AB,F2B与直线x=-$\frac{1}{2}$分别交于P,Q,R三个不同的点,且满足P,Q,R到x轴的距离依次成等比数列,求该直线l的方程.
分析 (Ⅰ)△AF1F2的周长为|AF1|+|AF2|+|F1F2|;
(Ⅱ)由题意得l不垂直两坐标轴,故设l的方程为y=k(x+1)(k≠0),因为P,Q,R到x轴的距离依次成等比数列,所以|yP|•|yR|=|yQ|2,联立y=k(x+1)与椭圆方程,消去y,利用韦达定理,即可得出结论.
解答 解:(Ⅰ)因为椭圆的长轴长2a=2$\sqrt{2}$,焦距2c=2.
又由椭圆的定义得|AF1|+|AF2|=2a
所以△AF1F2的周长为|AF1|+|AF2|+|F1F2|=2$\sqrt{2}$+2
(Ⅱ)由题意得l不垂直两坐标轴,故设l的方程为y=k(x+1)(k≠0)
于是直线l与直线x=-$\frac{1}{2}$交点Q的纵坐标为yQ=$\frac{k}{2}$
设 A(x1,y1),B(x2,y2),显然x1,x2≠1,
所以直线F2A的方程为y=$\frac{{y}_{1}}{{x}_{1}-1}$(x-1)
故直线F2A与直线x=-$\frac{1}{2}$交点P的纵坐标为yP=$\frac{-3{y}_{1}}{2({x}_{1}-1)}$
同理,点R的纵坐标为yR=$\frac{-3{y}_{2}}{2({x}_{2}-1)}$
因为P,Q,R到x轴的距离依次成等比数列,所以|yP|•|yR|=|yQ|2
即|$\frac{-3{y}_{1}}{2({x}_{1}-1)}$×$\frac{-3{y}_{2}}{2({x}_{2}-1)}$|=$\frac{{k}^{2}}{4}$
整理得9|x1x2+(x1+x2)+1|=|x1x2-(x1+x2)+1|.(*)
联立y=k(x+1)与椭圆方程,消去y得(1+2k2)x2+4k2x+2k2-2=0
所以x1+x2=$\frac{-4{k}^{2}}{1+2{k}^{2}}$,x1x2=$\frac{2{k}^{2}-2}{1+2{k}^{2}}$
代入(*)化简得|8k2-1|=9
解得k=±$\frac{\sqrt{5}}{2}$
经检验,直线l的方程为y═±$\frac{\sqrt{5}}{2}$(x+1).
点评 本题考查椭圆的定义,考查直线与椭圆的位置关系,考查学生的计算能力,属于中档题.

| A. | (1,4) | B. | (4,5) | C. | (1,5) | D. | (5,+∞) |
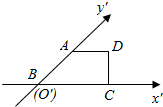 有一块多边形的菜地,它的水平放置的平面图形的斜二测直观图是直角梯形(如图)∠ABC=45°,AB=$\sqrt{2}$,AD=1,DC⊥BC,则这块菜地的面积为$3\sqrt{2}$.
有一块多边形的菜地,它的水平放置的平面图形的斜二测直观图是直角梯形(如图)∠ABC=45°,AB=$\sqrt{2}$,AD=1,DC⊥BC,则这块菜地的面积为$3\sqrt{2}$.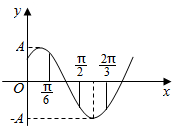 函数f(x)=Asin(ωx+φ)(A,ω,φ是常数,A>0,ω>0)的图象如图所示,若$f({\frac{π}{2}})=f({\frac{2π}{3}})=-f({\frac{π}{6}})$,则ω=2.
函数f(x)=Asin(ωx+φ)(A,ω,φ是常数,A>0,ω>0)的图象如图所示,若$f({\frac{π}{2}})=f({\frac{2π}{3}})=-f({\frac{π}{6}})$,则ω=2.