题目内容
4.在三棱锥A-BCD中,AB⊥平面BCD,CD⊥BD,AB=BD=CD=1,则该三棱锥外接球的表面积为3π.分析 由题意,三棱锥A-BCD扩充为长方体,其对角线长为$\sqrt{1+1+1}$=$\sqrt{3}$,可得三棱锥外接球的半径为$\frac{\sqrt{3}}{2}$,即可求出三棱锥外接球的表面积.
解答 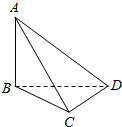 解:由题意,三棱锥A-BCD扩充为长方体,其对角线长为$\sqrt{1+1+1}$=$\sqrt{3}$,
解:由题意,三棱锥A-BCD扩充为长方体,其对角线长为$\sqrt{1+1+1}$=$\sqrt{3}$,
∴三棱锥外接球的半径为$\frac{\sqrt{3}}{2}$,
∴三棱锥外接球的表面积为4π•$(\frac{\sqrt{3}}{2})^{2}$=3π.
故答案为:3π.
点评 本题考查三棱锥外接球的表面积,三棱锥A-BCD扩充为长方体,求出三棱锥外接球的半径是关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
12.已知F是抛物线y2=4x的焦点,点A,B在该抛物线上且位于x轴的两侧,OA⊥OB(其中O为坐标原点),则△AOB与△AOF面积之和的最小值是( )
| A. | 16 | B. | 8$\sqrt{3}$ | C. | 8$\sqrt{5}$ | D. | 18 |
9.过点M(0,0),且平行于向量$\overrightarrow{a}$=(1,2)的直线方程是( )
| A. | x-2y=0 | B. | x+2y=0 | C. | 2x+y=0 | D. | 2x-y=0 |
14.下列说法中正确的是( )
| A. | 向量$\overrightarrow{a}$与非零向量$\overrightarrow{b}$共线,$\overrightarrow{b}$与$\overrightarrow{c}$共线,则$\overrightarrow{a}$与$\overrightarrow{c}$共线 | |
| B. | 任意两个相等向量不一定是共线向量 | |
| C. | 任意两个共线向量相等 | |
| D. | 若向量$\overrightarrow{a}$与$\overrightarrow{b}$共线,则$\overrightarrow{a}$=λ$\overrightarrow{b}$(λ>0) |