题目内容
3.在平面直角坐标系xOy中,已知△ABC的顶点A(-4,0)和C(4,0),顶点B在双曲线$\frac{x^2}{9}-\frac{y^2}{7}=1$上,则$\frac{sinA-sinC}{sinB}$=$±\frac{3}{4}$.分析 由题意可知双曲线的焦点坐标就是A,B,利用正弦定理以及双曲线的定义化简$\frac{sinA-sinC}{sinB}$,即可得到答案.
解答 解:由题意可知双曲线的焦点是A,B,
∵顶点B在双曲线$\frac{x^2}{9}-\frac{y^2}{7}=1$上,
∴由双曲线的定义可知||BC|-|AB||=2a=6,c=4,
∴$\frac{sinA-sinC}{sinB}$=$\frac{|BC|-|AB|}{|AC|}$=$±\frac{3}{4}$.
故答案为:$±\frac{3}{4}$.
点评 本题是基础题,考查双曲线的定义,正弦定理的应用,考查计算能力,常考题型.

练习册系列答案
相关题目
8.在△ABC中,A=30°,B=60°,C=90°,那么三边之比a:b:c等于( )
| A. | 1:2:3 | B. | 3:2:1 | C. | 1:$\sqrt{3}$:2 | D. | 2:$\sqrt{3}$:1 |
12.已知F是抛物线y2=4x的焦点,点A,B在该抛物线上且位于x轴的两侧,OA⊥OB(其中O为坐标原点),则△AOB与△AOF面积之和的最小值是( )
| A. | 16 | B. | 8$\sqrt{3}$ | C. | 8$\sqrt{5}$ | D. | 18 |
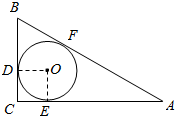 如图,在Rt△ABC中,∠C=90°,BC=a,AC=b,AB=c,⊙O为ABC的内切圆,D,E,F分别为切点,O的半径为r,试用含a,b,c的代数式表示r.
如图,在Rt△ABC中,∠C=90°,BC=a,AC=b,AB=c,⊙O为ABC的内切圆,D,E,F分别为切点,O的半径为r,试用含a,b,c的代数式表示r.