题目内容
已知F1,F2分别是椭圆的左,右焦点,现以F2为圆心作一个圆恰好经过椭圆中心并且交椭圆于点M,N,若过F1的直线MF1是圆F2的切线,则椭圆的离心率为( )
A、
| ||||
B、2-
| ||||
C、
| ||||
D、
|
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:由已知条件推导出|MF2|=c,|F1F2|=2c,∠F1MF2=90°,从而得到|MF1|=
c,由此能求出椭圆的离心率.
| 3 |
解答:
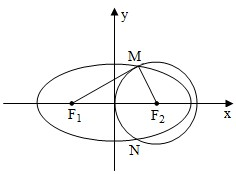 解:∵F1,F2分别是椭圆的左,右焦点,
解:∵F1,F2分别是椭圆的左,右焦点,
现以F2为圆心作一个圆恰好经过椭圆中心并且交椭圆于点M,N,
过F1的直线MF1是圆F2的切线,
∴|MF2|=c,|F1F2|=2c,∠F1MF2=90°,
∴|MF1|=
=
c,
∴2a=
c+c=(
+1)c,
∴椭圆的离心率e=
=
=
-1.
故选:A.
 解:∵F1,F2分别是椭圆的左,右焦点,
解:∵F1,F2分别是椭圆的左,右焦点,现以F2为圆心作一个圆恰好经过椭圆中心并且交椭圆于点M,N,
过F1的直线MF1是圆F2的切线,
∴|MF2|=c,|F1F2|=2c,∠F1MF2=90°,
∴|MF1|=
| 4c2-c2 |
| 3 |
∴2a=
| 3 |
| 3 |
∴椭圆的离心率e=
| c |
| a |
| 2 | ||
|
| 3 |
故选:A.
点评:本题考查椭圆的离心率的求法,是中档题,解题时要认真审题,注意数形结合思想的合理运用.

练习册系列答案
相关题目
已知集合A={x|x2-x<0},集合B={x|2x<4},则“x∈A”是“x∈B”的( )
| A、充分且不必要条件 |
| B、必要且不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
下面说法正确的是( )
| A、不存在既不是奇函数,有又不是偶函数的幂函数 |
| B、图象不经过点(-1,1)的幂函数一定不是偶函数 |
| C、如果两个幂函数的图象有三个公共点,那么这两个幂函数相同 |
| D、如果一个幂函数的图象不与y轴相交,则y=xα中α<0 |
设a=log210,b=log315,c=log735,则( )
| A、c>a>b |
| B、b>c>a |
| C、b>a>c |
| D、a>b>c |
设全集U=R,M={x|
<2x<1},N={x|ln(-x)>0},则M∩∁UN=( )
| 1 |
| 8 |
| A、{x|x≥-1} |
| B、{x|-3<x<0} |
| C、{x|x≤-3} |
| D、{x|-1≤x<0} |
执行如图所示的程序框图,若输入n的值为4,则输出s的值是( )


| A、2 | B、6 | C、24 | D、120 |
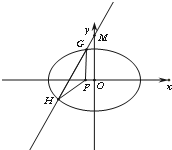 已知椭圆C:
已知椭圆C: 如图,已知焦点在x轴上的椭圆
如图,已知焦点在x轴上的椭圆