题目内容
在对某渔业产品的质量调研中,从甲、乙两地出产的该产品中各随机抽取10件,测量该产品中某种元素的含量(单位:毫克).如图是测量数据的茎叶图:

规定:当产品中的此种元素含量≥15毫克时为优质品.
(Ⅰ)试用上述样本数据估计甲、乙两地该产品的优质品率(优质品件数/总件数);
(Ⅱ)从乙地抽出的上述10件产品中,随机抽取3件,求抽到的3件产品中优质品数ξ的分布列及数学期望E(ξ).

规定:当产品中的此种元素含量≥15毫克时为优质品.
(Ⅰ)试用上述样本数据估计甲、乙两地该产品的优质品率(优质品件数/总件数);
(Ⅱ)从乙地抽出的上述10件产品中,随机抽取3件,求抽到的3件产品中优质品数ξ的分布列及数学期望E(ξ).
考点:离散型随机变量的期望与方差,茎叶图,古典概型及其概率计算公式
专题:概率与统计
分析:(I)由已知条件,利用古典概型概率的计算公式,能求出甲、乙两地该产品的优质品率.
(II)ξ的取值为1,2,3.分别求出其概率,由此能求出ξ的分布列和数学期望.
(II)ξ的取值为1,2,3.分别求出其概率,由此能求出ξ的分布列和数学期望.
解答:
解:(I)甲厂抽取的样本中优等品有7件,优等品率为
.
乙厂抽取的样本中优等品有8件,优等品率为
=
.…(4分)
(II)ξ的取值为1,2,3.…(5分)
…(7分)
P(ξ=2)=
=
,…(9分)
P(ξ=3)=
=
…(11分)
∴ξ的分布列为
…(12分)
∴ξ的数学期望为Eξ=1×
+2×
+3×
=
.…(13分)
| 7 |
| 10 |
乙厂抽取的样本中优等品有8件,优等品率为
| 8 |
| 10 |
| 4 |
| 5 |
(II)ξ的取值为1,2,3.…(5分)
|
P(ξ=2)=
| ||||
|
| 7 |
| 15 |
P(ξ=3)=
| ||||
|
| 7 |
| 15 |
∴ξ的分布列为
| ξ | 1 | 2 | 3 | ||||||
| P |
|
|
|
∴ξ的数学期望为Eξ=1×
| 1 |
| 15 |
| 7 |
| 15 |
| 7 |
| 15 |
| 12 |
| 5 |
点评:本题考查概率的计算,考查离散型随机变量的分布列和数学期望的求法,解题时要认真审题,注意排列组合的合理运用.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
设a=log210,b=log315,c=log735,则( )
| A、c>a>b |
| B、b>c>a |
| C、b>a>c |
| D、a>b>c |
执行如图所示的程序框图,若输入n的值为4,则输出s的值是( )


| A、2 | B、6 | C、24 | D、120 |
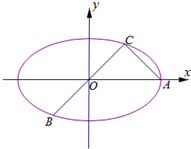 如图所示,已知A、B、C是长轴长为4的椭圆E上的三点,点A是长轴的一个端点,BC过椭圆中心O,且
如图所示,已知A、B、C是长轴长为4的椭圆E上的三点,点A是长轴的一个端点,BC过椭圆中心O,且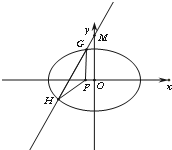 已知椭圆C:
已知椭圆C: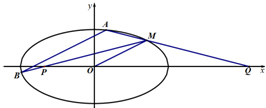 如图,已知离心率为
如图,已知离心率为