题目内容
7.已知等比数列{an}的首项a1=2013,公比q=-$\frac{1}{2}$,数列{an}前n项的积记为Tn,则使得Tn取得最大值时n的值为12.分析 根据等比数列的通项公式,求出Tn,然后利用作商法判断Tn单调性,即可得到结论.
解答 解:解:∵等比数列{an}的首项为a1=2015,公比q=-$\frac{1}{2}$,∴an=a1qn-1=2013(-$\frac{1}{2}$)n-1
∴当n为奇数时an>0,当n为偶数时,an<0,
∵当n≥2时,$\frac{{T}_{n}}{{T}_{n-1}}={a}_{n}=2013(-\frac{1}{2})^{n-1}$,
$|\frac{{T}_{n}}{{T}_{n-1}}|=2013•(\frac{1}{2})^{n-1}$
当n≤11时,$|\frac{{T}_{n}}{{T}_{n-1}}|$|f(n)|单调递增,当n≥12时,|f(n)|单调递减,
当n=11时,f(11)<0,
当n=12时,f(12)>0,
∴当n=12时,f(n)有最大值.
故答案为:12
点评 本题考查等比数列的通项公式,利用作商法判断单调性是解题的关键,综合性较强,难度较大,属于中档题.

练习册系列答案
相关题目
17.若点(1,-3)在圆(x-2)2+(y+1)2=m的内部,则实数m的取值范围是( )
| A. | 0<m<10 | B. | 0<m<5 | C. | m>5 | D. | m<5 |
2.$\frac{{tan{{18}°}+tan{{42}°}+tan{{120}°}}}{{tan{{198}°}tan{{222}°}}}$=( )
| A. | $-\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $-\frac{{\sqrt{3}}}{3}$ |
12.已知1,x,y,z,9成等比数列,则y=( )
| A. | -3 | B. | 3 | C. | 5 | D. | ±3 |
19.设区间[q,p]的长度为p-q,其中p>q.现已知两个区间[4lnm,ln2m]与[lnm,4lnm-10]的长度相等,则ex+1+me-x的最小值为( )
| A. | 2e3 | B. | $2{e^{\frac{3}{2}}}$或2e3 | C. | $2{e^{\frac{3}{2}}}$ | D. | $2{e^{\frac{3}{2}}}$或2e2 |
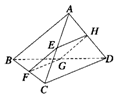 如图所示,四边形EFGH为空间四边形ABCD的一个截面,若CD∥面EFGH,求证:EH∥FG.
如图所示,四边形EFGH为空间四边形ABCD的一个截面,若CD∥面EFGH,求证:EH∥FG.