题目内容
在空间中,设α,β表示平面,m,n表示直线.则下列命题正确的是( )
| A、若m∥n,n⊥α,则m⊥α |
| B、若α⊥β,m?α,则m⊥β |
| C、若m上有无数个点不在α内,则m∥α |
| D、若m∥α,那么m与α内的任何直线平行 |
考点:空间中直线与平面之间的位置关系
专题:探究型,空间位置关系与距离
分析:对于A,据线面垂直的判定定理可知正确;对于B,列举出所以可能,可能是m与β不垂直;C:若直线与平面相交,则除了交点以外的任何一个点都不在平面内,这样的点有无数个;D:若直线l平行平面α,则l与平面α内的任意一条直线都没有公共点,所以l与平面α内的任一条直线有两种位置关系:平行、异面.
解答:
解:对于A,若m∥n,n⊥α,则m⊥α,据线面垂直的判定定理可知正确;
对于B,若α⊥β,m?α,则m⊥β;不正确,也可能是m与β不垂直,错误;
对于C,若直线与平面相交,则除了交点以外的无数个点都不在平面内,故错误;
对于D,若直线l平行平面α,则l与平面α内的任一条直线有两种位置关系:平行、异面,故错误,
故选:A.
对于B,若α⊥β,m?α,则m⊥β;不正确,也可能是m与β不垂直,错误;
对于C,若直线与平面相交,则除了交点以外的无数个点都不在平面内,故错误;
对于D,若直线l平行平面α,则l与平面α内的任一条直线有两种位置关系:平行、异面,故错误,
故选:A.
点评:本题考查空间直线与直线、直线与平面、以及平面与平面的位置关系,考查空间想象能力和逻辑推理能力.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
已知集合A={1,2,3},B={x|x≤2},则A∩B=( )
| A、∅ | B、{1} |
| C、{2} | D、{1,2} |
在△ABC中,若
=3,b2-a2=
ac,则cosB的值为( )
| sinC |
| sinA |
| 5 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
一个正三角形的外接圆的半径为1,向该圆内随机投一点P,点P恰好落在正三角形内的概率是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
复数
(i是虚数单位)化简的结果是( )
| 1-i |
| 1+i |
| A、1 | B、-1 | C、i | D、-i |
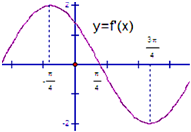 已知函数f(x)=Asin(x+φ)(A>0,0<φ<π),其导函数f′(x)的部分图形如图所示,则函数f(x)的解析式( )
已知函数f(x)=Asin(x+φ)(A>0,0<φ<π),其导函数f′(x)的部分图形如图所示,则函数f(x)的解析式( )A、f(x)=2sin(x+
| ||
B、f(x)=4sin(x+
| ||
C、f(x)=2sin(x+
| ||
D、f(x)=4sin(x+
|
