题目内容
已知函数f(x)=ex-ax,g(x)=b-sinx,F(x)=f(x)-g(x).
(1)当a=2时,对任意x1∈R,存在x2∈R,使f(x1)≥g(x2),求实数b的取值范围;
(2)若F(x)≥sin1-cos1-b对任意x≥0恒成立,求实数a的取值范围.
(1)当a=2时,对任意x1∈R,存在x2∈R,使f(x1)≥g(x2),求实数b的取值范围;
(2)若F(x)≥sin1-cos1-b对任意x≥0恒成立,求实数a的取值范围.
考点:导数在最大值、最小值问题中的应用,利用导数研究函数的单调性
专题:综合题,导数的综合应用
分析:(1)通过求导,令f'(x)>0,f'(x)<0,求出f(x)的单调性,从而得到f(x)的最小值,求出g(x)的最小值,由条件可知,只需f(x)min≥g(x)min,从而得到b的取值范围;
(2)原不等式ax≤ex+sinx-sin1+cos1对任意x≥0恒成立,对x=0,x>0讨论,运用参数分离,构造函数求导数,再构造函数求导数,从而得到原函数的单调性,求出最值,得出实数a的取值范围.
(2)原不等式ax≤ex+sinx-sin1+cos1对任意x≥0恒成立,对x=0,x>0讨论,运用参数分离,构造函数求导数,再构造函数求导数,从而得到原函数的单调性,求出最值,得出实数a的取值范围.
解答:
解:(1)当a=2时,f(x)=ex-2x,f'(x)=ex-2,
则x>ln2时,f'(x)>0,f(x)单调递增,x<ln2时,f(x)单调递减.
∴f(x)min=f(ln2)=2-2ln2,
又易知g(x)min=b-1,
对任意x1∈R,存在x2∈R,使得f(x1)≥g(x2),只需f(x)min≥g(x)min,
即2-2ln2≥b-1,∴b≤3-2ln2;
(2)F(x)≥sin1-cos1-b对任意x≥0恒成立,
即等价于ex-ax+sinx≥sin1-cos1对任意x≥0恒成立.
即ax≤ex+sinx-sin1+cos1对任意x≥0恒成立.
①若x=0,显然有a∈R,均有ax≤ex+sinx-sin1+cos1恒成立,
②若x>0,则即a≤
对x>0恒成立,
设h(x)=
,则只需a≤h(x)min,
又h'(x)=
,
设φ(x)=(x-1)ex+xcosx-sinx+sin1-cos1,知φ(1)=0,
φ'(x)=x(ex-sinx),∵x>0时,φ'(x)>0,∴φ(x)在(0,+∞)单调递增,
从而当x∈(0,1)时,φ(x)<0,当x∈(1,+∞)时,φ(x)>0,
故h(x)在(0,1)上递减,在(1,+∞)上递增.
∴h(x)min=h(1)=e+cos1,从而a≤e+cos1.
综上可知实数a的取值范围是(-∞,e+cos1].
则x>ln2时,f'(x)>0,f(x)单调递增,x<ln2时,f(x)单调递减.
∴f(x)min=f(ln2)=2-2ln2,
又易知g(x)min=b-1,
对任意x1∈R,存在x2∈R,使得f(x1)≥g(x2),只需f(x)min≥g(x)min,
即2-2ln2≥b-1,∴b≤3-2ln2;
(2)F(x)≥sin1-cos1-b对任意x≥0恒成立,
即等价于ex-ax+sinx≥sin1-cos1对任意x≥0恒成立.
即ax≤ex+sinx-sin1+cos1对任意x≥0恒成立.
①若x=0,显然有a∈R,均有ax≤ex+sinx-sin1+cos1恒成立,
②若x>0,则即a≤
| ex+sinx-sin1+cos1 |
| x |
设h(x)=
| ex+sinx-sin1+cos1 |
| x |
又h'(x)=
| (x-1)ex+xcosx-sinx+sin1-cos1 |
| x2 |
设φ(x)=(x-1)ex+xcosx-sinx+sin1-cos1,知φ(1)=0,
φ'(x)=x(ex-sinx),∵x>0时,φ'(x)>0,∴φ(x)在(0,+∞)单调递增,
从而当x∈(0,1)时,φ(x)<0,当x∈(1,+∞)时,φ(x)>0,
故h(x)在(0,1)上递减,在(1,+∞)上递增.
∴h(x)min=h(1)=e+cos1,从而a≤e+cos1.
综上可知实数a的取值范围是(-∞,e+cos1].
点评:本题主要考查导数在函数中的综合运用:求单调性,求极值和最值,考查不等式成立问题转化为求函数最值问题,以及参数分离和构造函数的重要思想方法,是一道综合题,属于难题.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
已知集合A={1,2,3},B={x|x≤2},则A∩B=( )
| A、∅ | B、{1} |
| C、{2} | D、{1,2} |
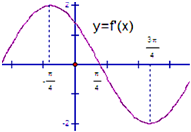 已知函数f(x)=Asin(x+φ)(A>0,0<φ<π),其导函数f′(x)的部分图形如图所示,则函数f(x)的解析式( )
已知函数f(x)=Asin(x+φ)(A>0,0<φ<π),其导函数f′(x)的部分图形如图所示,则函数f(x)的解析式( )A、f(x)=2sin(x+
| ||
B、f(x)=4sin(x+
| ||
C、f(x)=2sin(x+
| ||
D、f(x)=4sin(x+
|
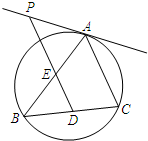 如图,△ABC内接于圆O,D为弦BC上一点,过D作直线DP∥AC,交AB于点E,交圆O
如图,△ABC内接于圆O,D为弦BC上一点,过D作直线DP∥AC,交AB于点E,交圆O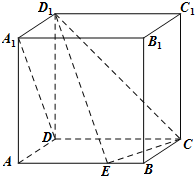 如图,在棱长为1的正方体ABCD-A1B1C1D1中,点E是棱AB上的动点.
如图,在棱长为1的正方体ABCD-A1B1C1D1中,点E是棱AB上的动点.