题目内容
已知函数f(x)＝|x－7|－|x－3|.
(1)作出函数f(x)的图象；
(2)当x<5时，不等式|x－8|－|x－a|>2恒成立，求a的取值范围．
(1)∵f(x)＝
图象如图所示：
(2)∵x<5，∴|x－8|－|x－a|>2，即8－x－|x－a|>2，
即|x－a|<6－x，对x<5恒成立．
即x－6<x－a<6－x对x<5恒成立，
∴
对x<5恒成立．
又∵x<5时，2x－6<4，∴4≤a<6.
∴a的取值范围为[4,6)．
练习册系列答案
相关题目
(t为参数)．
)＝
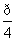a，曲线C2的参数方程为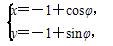
(φ为参数，0≤φ≤π)．