题目内容
在直角坐标系xOy中，以O为极点，x轴正半轴为极轴建立极坐标系，曲线C1的极坐标方程为ρsin(θ＋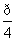
)＝
a，曲线C2的参数方程为
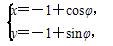(φ为参数，0≤φ≤π)．
(1)求C1的直角坐标方程；
(2)当C1与C2有两个不同公共点时，求实数a的取值范围．
[解析] (1)将曲线C1的极坐标方程变形，
ρ(sinθ＋cosθ)＝a，
即ρcosθ＋ρsinθ＝a，
∴曲线C1的直角坐标方程为x＋y－a＝0.
(2)曲线C2的直角坐标方程为(x＋1)2＋(y＋1)2＝1(－1≤y≤0)，为半圆弧，
如图所示，曲线C1为一组平行于直线x＋y＝0的直线，
当直线C1与C2相切时，由
＝1得a＝－2±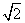
，
舍去a＝－2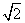－，得a＝－2＋，
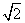当直线C1过A(0，－1)、B(－1,0)两点时，a＝－1.
∴由图可知，当－1≤a<－2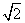＋时，曲线C1与曲线C2有两个公共点．
练习册系列答案
相关题目
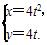(t为参数)上，则|PF|＝( )
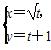(t为参数)，曲线C2的极坐标方程为ρsinθ－ρcosθ＝3，则C1与C2的交点在直角坐标系中的坐标为________．
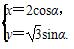(α为参数)，在极坐标系(与直角坐标系xOy取相同的长度单位，且以原点O为极点，以x轴正半轴为极轴)中，曲线C2的方程为ρ(cosθ－sinθ)＋1＝0，则C1与C2的交点个数为________．
<
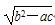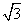a”“索”的“因”应是( )