题目内容
若函数y=
的定义域为R，则实数m的取值范围是（ ）
| m(x+1)-2 | |||
|
A、（0，
| ||
B、（0，
| ||
C、[0，
| ||
D、[0，
|
考点：函数的定义域及其求法
专题：函数的性质及应用
分析：根据函数的定义域，建立条件关系即可得到结论．
解答：
解：∵函数y=
的定义域为R，
∴mx2+4mx+3≠0，
若m=0，则不等式等价为3≠0，成立，
若m≠0，则不等式等价为判别式△=16m2-4×3m＜0，
即4m2-3m＜0，则0＜m＜
，
综上：0≤m＜
，
故选：D
| m(x+1)-2 | |||
|
∴mx2+4mx+3≠0，
若m=0，则不等式等价为3≠0，成立，
若m≠0，则不等式等价为判别式△=16m2-4×3m＜0，
即4m2-3m＜0，则0＜m＜
| 3 |
| 4 |
综上：0≤m＜
| 3 |
| 4 |
故选：D
点评：本题主要考查函数定义域的应用，注意要对m进行讨论．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，边长为a的等边三角形ABC的中线AF与中位线DE交于点G，已知△A′DE（A′∉平面ABC）是△ADE绕DE旋转过程中的一个图形，有下列命题：①平面A′FG⊥平面ABC；
②BC∥平面A′DE；
③三棱锥A′-DEF的体积最大值为
| 1 |
| 64 |
④存在某个位置，使得DF与A′E垂直．
其中正确的命题是（ ）
| A、② | B、②③ |
| C、①②③ | D、①②③④ |
若z1=a+2i，z2=3-4i，且
为纯虚数，则实数a的值是（ ）
| z1 |
| z2 |
| A、2 | ||
B、
| ||
C、
| ||
| D、3 |
归纳推理是（ ）
| A、特殊到一般的推理 |
| B、特殊到特殊的推理 |
| C、一般到特殊的推理 |
| D、一般到一般的推理 |
如图，该程序运行后的输出结果为（ ）
| A、0 | B、3 | C、12 | D、-2 |
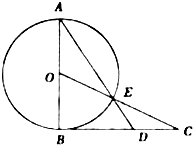如图，AB为⊙O的直径，过点B作⊙O的切线BC，OC交⊙O于点E，AE的延长线交BC于点D．