题目内容
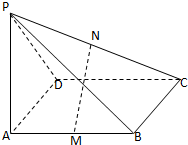如图所示，ABCD是矩形，PA⊥平面ABCD，△PAD是等腰三角形，M、N分别是AB、PC的中点．求证：MN⊥平面PCD．（向量法证明）考点：直线与平面垂直的判定
专题：空间位置关系与距离
分析：建立空间直角坐标系A-xyz，得到
，
，
的坐标，利用向量的数量积判断．
| CD |
| DP |
| MN |
解答：
解：建立坐标系如图，
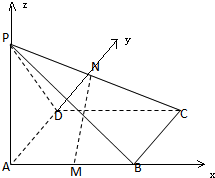
设AB=2a，AD=2b，ABCD是矩形，PA⊥平面ABCD，△PAD是等腰三角形，M、N分别是AB、PC的中点．
所以P（0，0，2b），D（0，2b，0），C（2a，2b，0），M（a，0，0），N（a，b，b），
所以
=（2a，0，0），
=（0，2b，-2b），
=（0，b，b），
•
=0，
•
=0，
所以CD⊥MN，DP⊥MN，
所以MN⊥平面PCD．
设AB=2a，AD=2b，ABCD是矩形，PA⊥平面ABCD，△PAD是等腰三角形，M、N分别是AB、PC的中点．
所以P（0，0，2b），D（0，2b，0），C（2a，2b，0），M（a，0，0），N（a，b，b），
所以
| CD |
| DP |
| MN |
| CD |
| MN |
| DP |
| MN |
所以CD⊥MN，DP⊥MN，
所以MN⊥平面PCD．
点评：本题考查了利用向量法求证线面垂直，关键是适当建系，正确写出所需的向量坐标，利用向量的数量积解答．
练习册系列答案
开心练习课课练与单元检测系列答案
开心试卷期末冲刺100分系列答案
相关题目
给出四个函数，分别满足①f（x+y）=f（x）+f（y）；②g（x+y）=g（x）•g（y）；③ϕ（x•y）=ϕ（x）+ϕ（y）；④ω（x•y）=ω（x）•ω（y），又给出四个函数的图象如下：
则正确的配匹方案是（ ）
则正确的配匹方案是（ ）
| A、①-M ②-N ③-P ④-Q |
| B、①-N ②-P ③-M ④-Q |
| C、①-P ②-M ③-N ④-Q |
| D、①-Q ②-M ③-N ④-P |
下列命题正确的是（ ）
| A、若a＞b＞1，c＜0，则ae＞be | ||||
| B、若|a|＞b，则a2＞b2 | ||||
C、?x0∈R，x0+
| ||||
D、若a＞0，b＞0且a+b=1，则
|
已知f（x）是奇函数，且f（x+2）=f（x），当0≤x≤1时，f（x）=2x（1-x），则f（-
）=（ ）
| 5 |
| 2 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|