题目内容
对某交通要道以往的日车流量(单位:万辆)进行统计,得到如下记录:
将日车流量落入各组的频率视为概率,并假设每天的车流量相互独立.
(Ⅰ)求在未来连续3天里,有连续2天的日车流量都不低于10万辆且另1天的日车流量低于5万辆的概率;
(Ⅱ)用X表示在未来3天时间里日车流量不低于10万辆的天数,求X的分布列和数学期望.
| 日车流量x | 0≤x<5 | 5≤x<10 | 10≤x<15 | 15≤x<20 | 20≤x<25 | x≥25 |
| 频率 | 0.05 | 0.25 | 0.35 | 0.25 | 0.10 | 0 |
(Ⅰ)求在未来连续3天里,有连续2天的日车流量都不低于10万辆且另1天的日车流量低于5万辆的概率;
(Ⅱ)用X表示在未来3天时间里日车流量不低于10万辆的天数,求X的分布列和数学期望.
考点:离散型随机变量及其分布列,离散型随机变量的期望与方差
专题:概率与统计
分析:(Ⅰ)设A1表示事件“日车流量不低于10万辆”,A2表示事件“日车流量低于5万辆”,B表示事件“在未来连续3天里有连续2天日车流量不低于10万辆且另1天车流量低于5万辆”.直接求出概率即可.
(Ⅱ)X可能取的值为0,1,2,3,求出相应的概率,写出X的分布列,即可求出E(X).
(Ⅱ)X可能取的值为0,1,2,3,求出相应的概率,写出X的分布列,即可求出E(X).
解答:
解:(Ⅰ)设A1表示事件“日车流量不低于10万辆”,A2表示事件“日车流量低于5万辆”,B表示事件“在未来连续3天里有连续2天日车流量不低于10万辆且另1天车流量低于5万辆”.则
P(A1)=0.35+0.25+0.10=0.70,P(A2)=0.05,
所以P(B)=0.7×0.7×0.05×2=0.049.
(Ⅱ)X可能取的值为0,1,2,3,相应的概率分别为P(X=0)=
•(1-0.7)3=0.027,P(X=1)=
•0.7•(1-0.7)2=0.189,P(X=2)=
•0.72•(1-0.7)=0.441,P(X=3)=
•0.73=0.343.
X的分布列为
因为X~B(3,0.7),所以期望E(X)=3×0.7=2.1.
P(A1)=0.35+0.25+0.10=0.70,P(A2)=0.05,
所以P(B)=0.7×0.7×0.05×2=0.049.
(Ⅱ)X可能取的值为0,1,2,3,相应的概率分别为P(X=0)=
| C | 0 3 |
| C | 1 3 |
| C | 2 3 |
| C | 3 3 |
X的分布列为
| X | 0 | 1 | 2 | 3 |
| P | 0.027 | 0.189 | 0.441 | 0.343 |
点评:本题考查离散型随机变量的分布列的期望与方差,考查计算能力.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
下列说法中正确的是( )
①f(x)=x0与g(x)=1是同一个函数;
②y=f(x)与y=f(x+1)有可能是同一个函数;
③y=f(x)与y=f(t)是同一个函数;
④定义域和值域相同的函数是同一个函数.
①f(x)=x0与g(x)=1是同一个函数;
②y=f(x)与y=f(x+1)有可能是同一个函数;
③y=f(x)与y=f(t)是同一个函数;
④定义域和值域相同的函数是同一个函数.
| A、①② | B、②③ | C、②④ | D、①③ |
已知函数f(x)是R上的增函数,A(0,-1),B(3,1)是其图象上的两点,那么f(x+1)<1的解集的补集是( )
| A、(-1,2) |
| B、(1,4) |
| C、[2,+∞) |
| D、[4,+∞) |

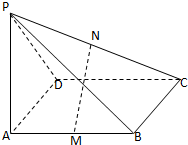 如图所示,ABCD是矩形,PA⊥平面ABCD,△PAD是等腰三角形,M、N分别是AB、PC的中点.求证:MN⊥平面PCD.(向量法证明)
如图所示,ABCD是矩形,PA⊥平面ABCD,△PAD是等腰三角形,M、N分别是AB、PC的中点.求证:MN⊥平面PCD.(向量法证明)