题目内容
已知f(x)是奇函数,且f(x+2)=f(x),当0≤x≤1时,f(x)=2x(1-x),则f(-
)=( )
| 5 |
| 2 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:当0≤x≤1时,f(x)=2x(1-x),可得f(
).由于f(x+2)=f(x),可得f(-
)=f(-
).由于f(x)是奇函数,可得f(-
)=-f(
).
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:∵当0≤x≤1时,f(x)=2x(1-x),
∴f(
)=2×
×(1-
)=
.
∵f(x+2)=f(x),∴f(-
)=f(-
).
∵f(x)是奇函数,
∴f(-
)=-f(
)=-
.
∴f(-
)=-
.
故选:D.
∴f(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵f(x+2)=f(x),∴f(-
| 5 |
| 2 |
| 1 |
| 2 |
∵f(x)是奇函数,
∴f(-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴f(-
| 5 |
| 2 |
| 1 |
| 2 |
故选:D.
点评:本题考查了函数的奇偶性、周期性,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
某单位有职工75人,其中青年职工35人,中年职工25人,老年职工15人,为了了解该单位职工的健康情况,用分层抽样的方法从中抽取样本,若样本容量为15,则样本中的青年职工人数为( )
| A、7 | B、15 | C、25 | D、35 |
 如图,矩形ABCD的四个顶点的坐标分别为A(0,-1),B(π,-1),C(π,1),D(0,1),正弦曲线f(x)=sinx和余弦曲线g(x)=cosx在矩形ABCD内交于点F,向矩形ABCD区域内随机投掷一点,则该点落在阴影区域内的概率是( )
如图,矩形ABCD的四个顶点的坐标分别为A(0,-1),B(π,-1),C(π,1),D(0,1),正弦曲线f(x)=sinx和余弦曲线g(x)=cosx在矩形ABCD内交于点F,向矩形ABCD区域内随机投掷一点,则该点落在阴影区域内的概率是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列算法中,含有条件分支结构的是( )
| A、求两个数的积 |
| B、求点到直线的距离 |
| C、解一元二次不等式 |
| D、已知梯形两底和高求面积 |
设{an}是首项为-
,公差为d(d≠0)的等差数列,Sn为其前n项和,若S1,S2,S4成等比数列,则d=( )
| 1 |
| 2 |
| A、-1 | ||
B、-
| ||
C、
| ||
D、
|
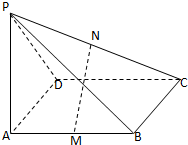 如图所示,ABCD是矩形,PA⊥平面ABCD,△PAD是等腰三角形,M、N分别是AB、PC的中点.求证:MN⊥平面PCD.(向量法证明)
如图所示,ABCD是矩形,PA⊥平面ABCD,△PAD是等腰三角形,M、N分别是AB、PC的中点.求证:MN⊥平面PCD.(向量法证明)